[技術連載]
5G時代の先進ミリ波ディジタル無線実験室
[Vol.5 高周波センスを磨く！スミス・チャート]

次世代高速移動通信と高分解能レーダのキー・テクノロジ

• 著者・講師：株式会社ラジアン（加藤 隆志/Takashi Katou）
• 企画編集・主催： ZEPエンジニアリング株式会社


• 関連製品：［KIT］ミリ波5G対応アップ・ダウン・コンバータ MkⅡ（mz-mmcon1後継機）
• 関連製品：［KIT］ミリ波5G対応アップ：ダウン・コンバータ（生産終了品）
• 関連製品：［KIT］実験用800M～6GHz 広帯域90°ハイブリッド
• 関連製品：［KIT］実験用27.5G-29.5GHzバンド・パス・フィルタ
• 関連製品：［KIT］実験用28GHzミリ波パッチ・アンテナ
• 関連製品：［VOD/KIT］GPSクロック・ジッタ・クリーナ
• 関連製品：［VOD］MATLAB/Simulink×FPGAで作るUSBスペクトラム・アナライザ
• 関連製品：［VOD/KIT］3GHzネットアナ付き！RF回路シミュレーション＆設計・測定入門
• 関連製品：［VOD/KIT］3GHzネットアナ付き！初めてのIoT向け基板アンテナ設計
• 関連製品：［VOD/KIT］初めてのソフトウェア無線＆信号処理プログラミング 基礎編/応用編
• 関連製品：［VOD］Pythonで学ぶ マクスウェル方程式 【電場編】＋【磁場編】
• 関連製品：［VOD］Pythonで学ぶ やりなおし数学塾1【微分・積分】
• 関連製品：［VOD］Pythonで学ぶ やりなおし数学塾2【フーリエ解析】
• 関連記事：超長距離無線LoRaからローカル5Gまで！GNU Radio×USRPで作るソフトウェア無線機

【Index】

• Vol.1　ミリ波の性質と広帯域通信の実験環境
• Vol.2　反射の起こらない線路を作る
• Vol.3　電磁波の漏れが少ない伝送線路
• Vol.4　信号が減衰しない基板
• Vol.5　高周波センスを磨く！スミス・チャート
• Vol.6　部品や伝送線路の入出力特性モデル「$S$パラメータ」
• Vol.7　高速データ伝送 成功の鍵「群遅延」
• Vol.8　初めての28GHzミリ波伝搬実験
• Vol.9　帯域優先？精度優先？2種類の周波数変換方式

超低$C/N$！mz-mmcon1 後継機 z-mmcon2 誕生

写真Aに示すのは，1台でミリ波を使ったディジタル無線通信が可能な$I/Q$変調＆周波数コンバータ“z-mmcon2”(開発：ラジアン)です．ミリ波5G対応アップ・ダウン・コンバータ mz-mmcon1の後継機です．

スペック

1. 送信周波数範囲：24.0G～44.0GHz
2. 送信出力範囲：+10～-29dBm（信号の条件 CW）
3. 送信ゲイン範囲：+20～-19dB（$I/Q$動作時）
4. 受信周波数範囲：24.0G～44.0GHz
5. 受信入力範囲-：10dBm以下（信号の条件 CW）
6. 受信ゲイン範囲：+12～-9dB（$I/Q$動作時）
7. 受信雑音指数：10dB以下
8. ベースバンド周波数範囲：DC～100kHz（内蔵D-Aコンバータ，外部アクセス不可）
9. ベースバンド・レベル範囲：0dBm以下（内蔵D-Aコンバータ，外部アクセス不可）
10. IF周波数範囲：1G～6GHz（本体背面のSMA端子）
11. IFレベル範囲：0dBm以下（本体背面のSMA端子）
12. 電源：付属のACアダプタ（DC6V，2A）
13. 消費電流：1.5A（通常動作時）
14. 基板サイズ：128×93×1.6mm（基材はRogers4350B）
15. ケース・サイズ：$W$=140mm $D$=129mm $H$=40mm（フランジ含む）

従来品 ミリ波5G対応アップ・ダウン・コンバータ mz-mmcon1からの改善点

z-mmcon2（写真A ）は，従来機のmz-mmcon1から，下記の点が改良されています．

1. 周波数範囲の拡大（27GHz～43GHz → 24GHz～44GHz）
2. シンセサイザICの変更（ADF4372）に伴う$C/N$の大幅改善
3. 制御をWindowsアプリからターミナルに変更（FTDIドライバに起因するトラブル回避）
4. 外部機器との接続をIF（1G～6GHz）だけに変更
5. 放熱ケース採用とファンレス化，ケースの大型化
6. USBマイクロをUSB-Bに変更（コネクタ破壊対策）

スミス・チャート脳トレ

抵抗やコンデンサやコイルのふるまいがわからなければ，どのような定数のどんなタイプのものをいくつ，どのように(並列？直接？)接続すれば，自分のイメージどおりに動く電子回路になるのか想像もつきません．こんな状態では，何百万円の優れたツールやシミュレータをもっていても，パソコンの画面を見つめるだけで回路設計は一歩も前に進みません．

特に高周波の分野では，周波数によって回路や線路のインピーダンスが$∞～0Ω$の範囲でぐるぐる大きく変化します．無線機や計測器の設計現場では，使う周波数や必要な帯域をまず決めて，その範囲で回路や伝送線路が希望のインピーダンスに近くなるように調整します．この設計作業を「インピーダンス・マッチング」と呼びます．

インピーダンス・マッチングに成功するためには，ターゲットにコンデンサやインダクタを追加したときに，もとのインピーダンスがどのように変化していくのかを見通す力が必要です．

これができなければ，方針を決めることができず，パソコンや回路図の前でボーっとするしかありません．答えは1つではありませんから，藪から棒にシミュレータに対策回路を入れてみて結果オーライを目指してもかまいませんが，1～2個の部品追加で済むところを，たくさんの部品をべたべた加えることとなり，ロスが増えて感度の低下を招いたりするでしょう．メカニズムを理解していてやりたいことがはっきり見えている人だけが，低コストで高性能を両立できる“simple is best”な答えにたどり着くことができます．

今回は，そんなセンスのいい高周波設計力が身に着く，交流インピーダンスの可視化ツール「スミス・チャート」の使い方を解説します．周波数によって大きく変化するインピーダンスを1つの円内に描くことができる今も昔も未来にも，高周波センスアップ用の貴重な脳トレ・ツールです．〈ZEPマガジン編集部〉

スミス・チャートを使えば高周波への道が開ける

マイクロ波($300 \mathrm{M}～30\mathrm{GHz}$)やミリ波($30\mathrm{G}～300\mathrm{GHz}$)を扱う高周波回路や基板を設計するときは，次の3つのパラメータを使いこなします．

1. インピーダンス
2. 反射
3. $S$パラメータ

これらの値は，周波数とともダイナミックに変化します．

今回は，その軌跡を1つの円上に描くツール「スミス・チャート」を紹介します．80年以上前に誕生した古い高周波回路の設計ツールです．

スミス・チャートを使い倒せば，測定器やシミュレータがなくても，脳内でインピーダンスの地図を作れるようになります．その結果，高周波回路シミュレータも上手に乗りこなせるようになります．

あなたの知らない高周波の世界

高周波では「周波数」と「インピーダンス」は切れない関係

電子回路を設計する技術者の多くは，DC～オーディオ帯域の低い周波数から始めて，高周波へと時間をかけて知識を深めていきます．これは高周波になるほど，考慮すべきパラメータが増えて複雑になるからです．

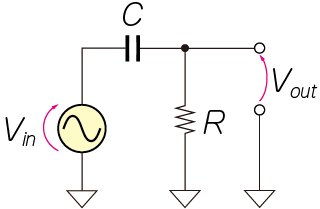
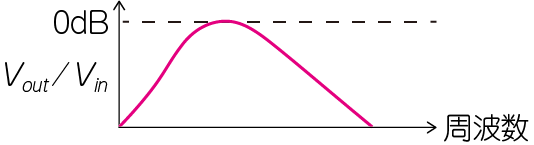
低周波回路の技術者は「抵抗とシリーズにコンデンサを入れたら低域がカットされるはず」と考えるでしょう[図1(a)(b)]．しかし高周波回路の技術者は「抵抗とシリーズにコンデンサを入れたら，ゲインが増すこともあるかもしれない[図1(c)]」と見ます．

これは高周波では，交流インピーダンスが周波数によって大きく変動することが大前提だからです．逆に言うと，周波数を規定しないと，インピーダンスの議論は始まりません．

周波数とインピーダンスが切り離されて議論されることが多い低周波回路の設計しか経験のない技術者が高周波回路に手を出すと，「何やこれ，ワケがわからん．やってみなくちゃわからない」と出口のない状態に陥るでしょう．

この混沌から抜け出すためには，交流インピーダンスの知識とその動きを捕らえる手段が必要です．

低周波の知識だけでは理解できない実際に起こる高周波現象

$5\mathrm{GHz}$で$-1\mathrm{dB}$のLPF特性もつRF ICを例に

手始めに，「スミス・チャート」を使ってインダクタとコンデンサのインピーダンスの周波数変化をプロットしてみましょう．

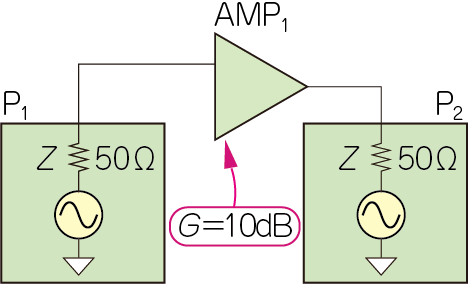
図2に示すのは，高周波アンプ($\mathrm{AMP}_1$)のゲインの周波数特性を測る回路です．

$\mathrm{P}_1$は，信号発生器(SG，Signal Generater)で，$1\mathrm{G}～10\mathrm{GHz}$の範囲で変化させることができます．$\mathrm{P}_2$はパワー・メータです．$\mathrm{P}_1$と$\mathrm{P}_2$の内部インピーダンスはどちらも$50\mathrm{Ω}$です．

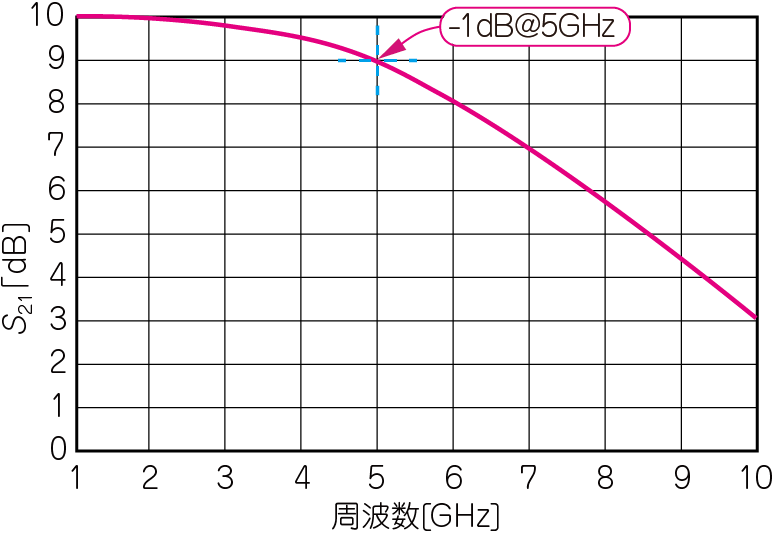
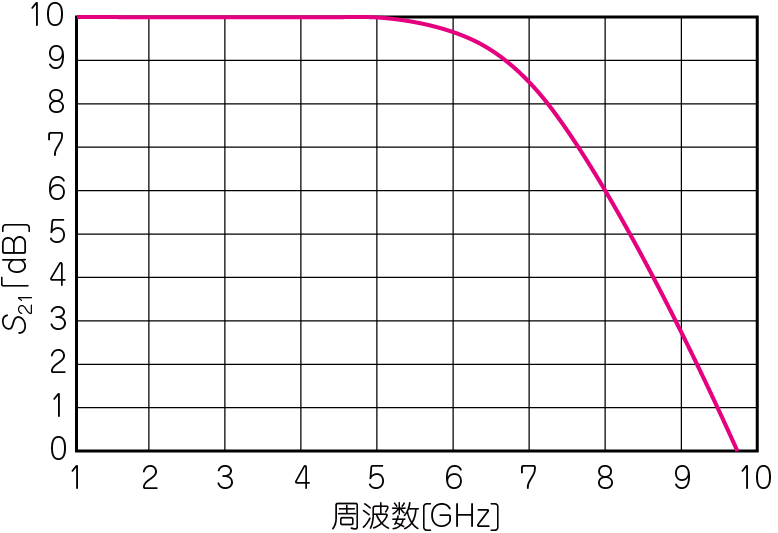
さて，内部回路の不明なブラックボックス $\mathrm{AMP}_1$のゲインの周波数特性を測ってみたところ，図3のような結果が得られました．高域になるほどゲインが低下する増幅器の典型的な特性です．

$\mathrm{AMP}_1$と直列に$0.7\mathrm{pF}$を追加

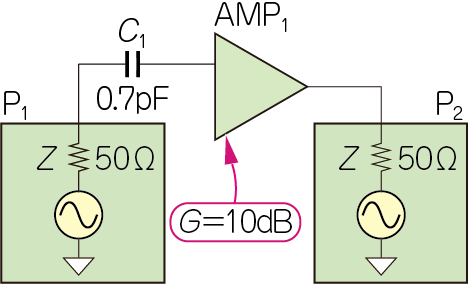
目標は，フラットなゲイン特性ではなく，$5\mathrm{GHz}$で最大にすることです．図4に示すように，$\mathrm{AMP}_1$の入力にシリーズにコンデンサ($C_1$)を追加してみます．

$C_1$の定数をあれこれ変えながら周波数特性を測りまくると，$0.7 \mathrm{pF}$でゲインが最大になります(図5)．

$\mathrm{AMP}_1$と並列に$2.2\mathrm{nH}$を追加する

まだゲインを上げる余地があります．

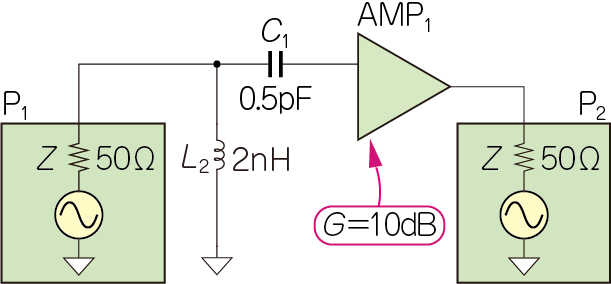
図6に示すように，信号ラインとグラウンドの間にインダクタ($L_2$)を追加します．

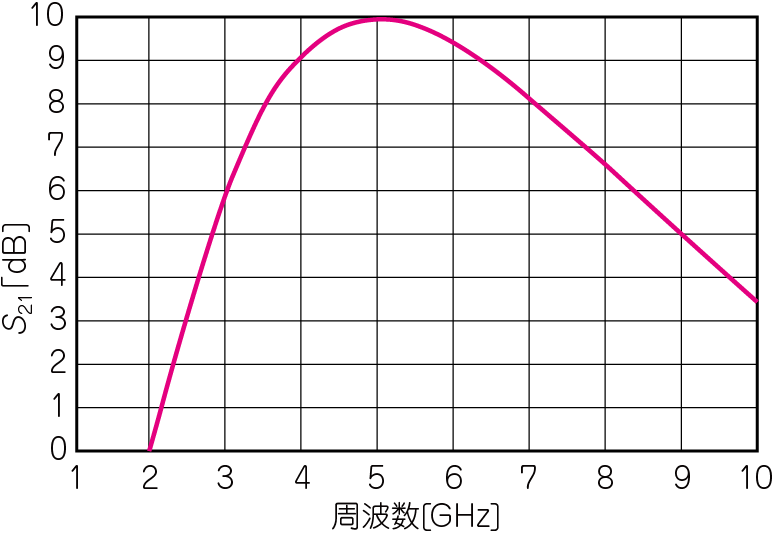
$L_1$と$C_1$の定数をあれこれ変えながら周波数特性の測定を繰り返すと，$C_1=0.5 \mathrm{pF}$，$L_2=2\mathrm{nH}$のとき，ゲインが最大になります(図7)．図5より，少しだけ改善しました．

$C_1$の容量を小さくして($0.7\mathrm{pF}→0.5\mathrm{pF}$)，$L_2$を加えたわけですから，ゲインは下がるように思うかもしれませんが，結果は逆です．図3と図7の$5\mathrm{GHz}$のときのゲインを比べると，約$1\mathrm{dB}$増しています．

これは，高周波回路では普通に起こる現象です．

種明かし

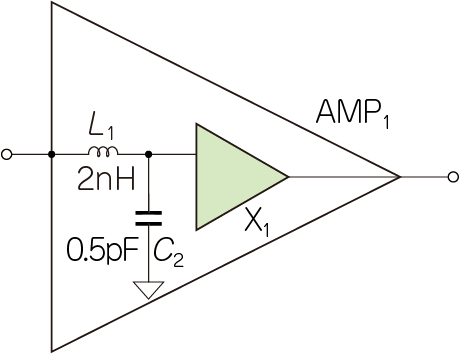
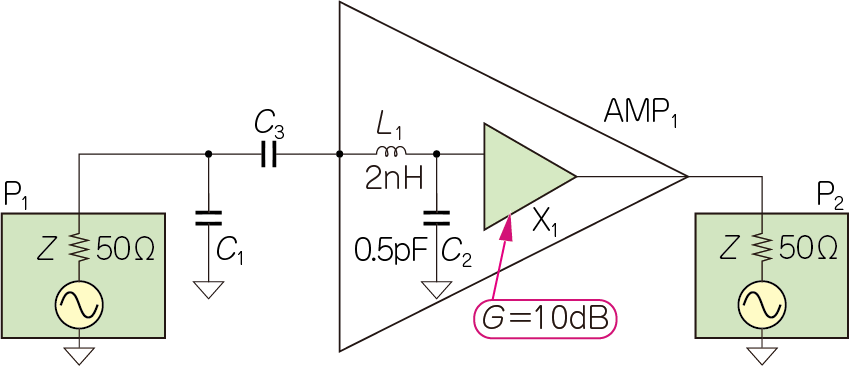
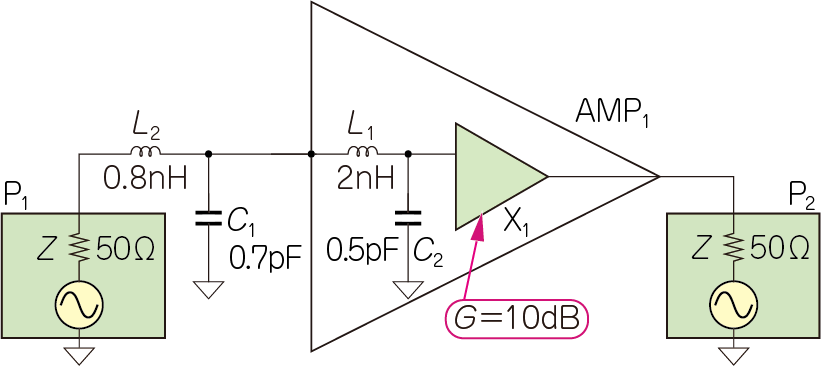
図8に示すのは，$\mathrm{AMP}_1$内部の等価回路です．

$\mathrm{X}_1$は理想アンプです．理想アンプの入力インピーダンスと出力インピーダンスは$50\mathrm{Ω}$で，入力と出力のアイソレーションは無限大です．またゲインは全周波数において$10\mathrm{dB}$でフラットです．

実際の$\mathrm{AMP}_1$には，入力部にインダクタ $L_1(2\mathrm{nH})$がシリーズに，$C_2=0.5 \mathrm{pF}$が並列に接続されています．リード・フレームとボンディング・ワイヤで$2\mathrm{nH}$，増幅ICのベア・チップの入力容量を$0.5 \mathrm{pF}$としています．これは，一般的なマイクロ波表面実装アンプICの入力インピーダンスを再現した構成です．

図6で追加した$0.5\mathrm{pF}$のコンデンサと$2.2\mathrm{nH}$のインダクタは，$5\mathrm{GHz}$において，$\mathrm{AMP}_1$内部(図7)にあるインダクタとコンデンサの影響を打ち消して見えなくしていたのです．

この調整作業のことを「インピーダンス・マッチング」と呼びます．

スミス・チャートの読み方

$\mathrm{AMP}_1$の入力インピーダンス

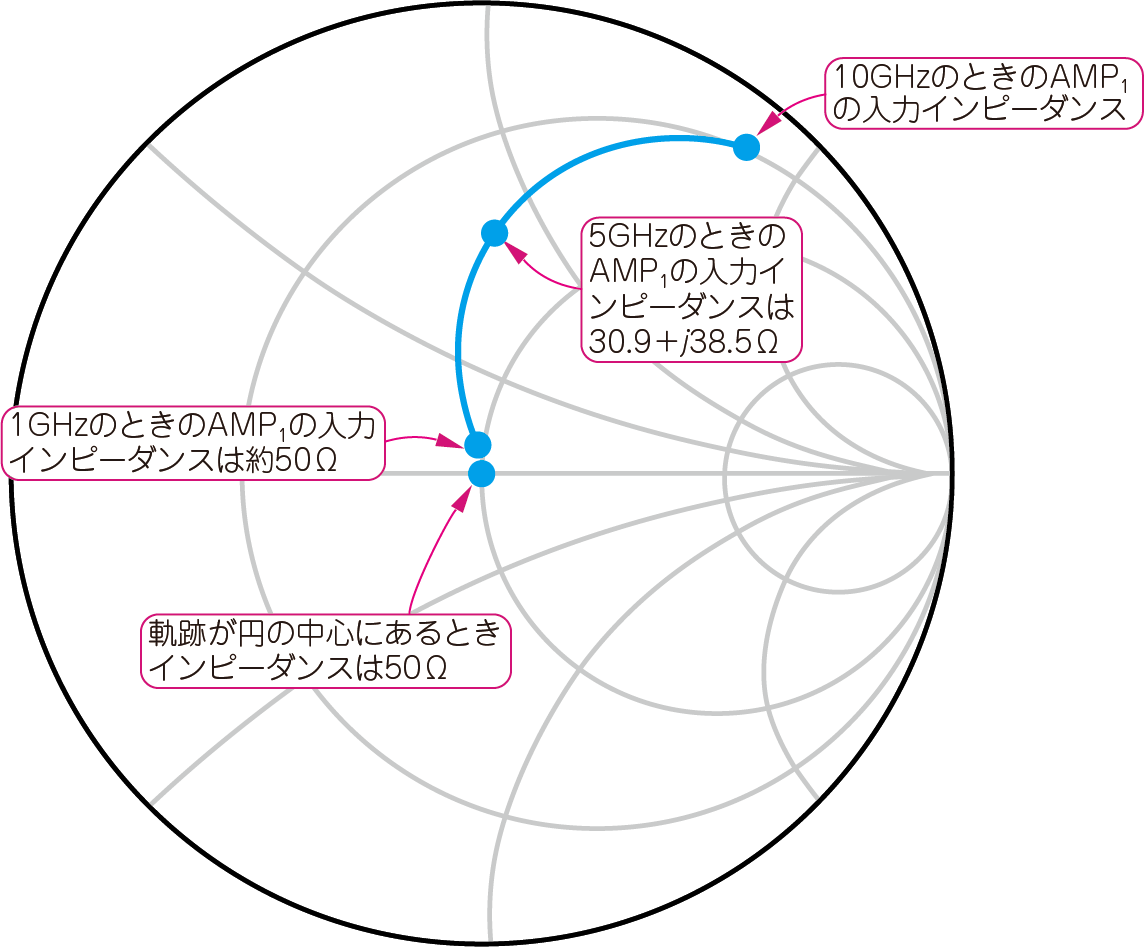
図9に示すのは，$\mathrm{AMP}_1$の入力インピーダンスの周波数変化($1\mathrm{G}～10\mathrm{GHz}$)です．これがスミス・チャートです．

まず，スミス・チャートの中心点を$50\mathrm{Ω}$と定義します(測定器や伝送路が$50\mathrm{Ω}$系の場合)．これを「$50\mathrm{Ω}$で正規化する」と言います．

スミス・チャート上には，周波数で変化するインピーダンスの軌跡がプロットされています(青色の実線)．$1\mathrm{GHz}$における入力インピーダンスは約$50\mathrm{Ω}$ですが，$5\mathrm{GHz}$では大きく外れています．これはロスが大きく，ゲインが低下することを示しています．

$\mathrm{AMP}_1$の入力インピーダンスのデータは，つまり，図9のインピーダンス軌跡はデバイスのデータシートから得ることができます．あるいは，ネットワーク・アナライザを使って自分で実測します．

プロット位置からインピーダンスや反射率が一目瞭然

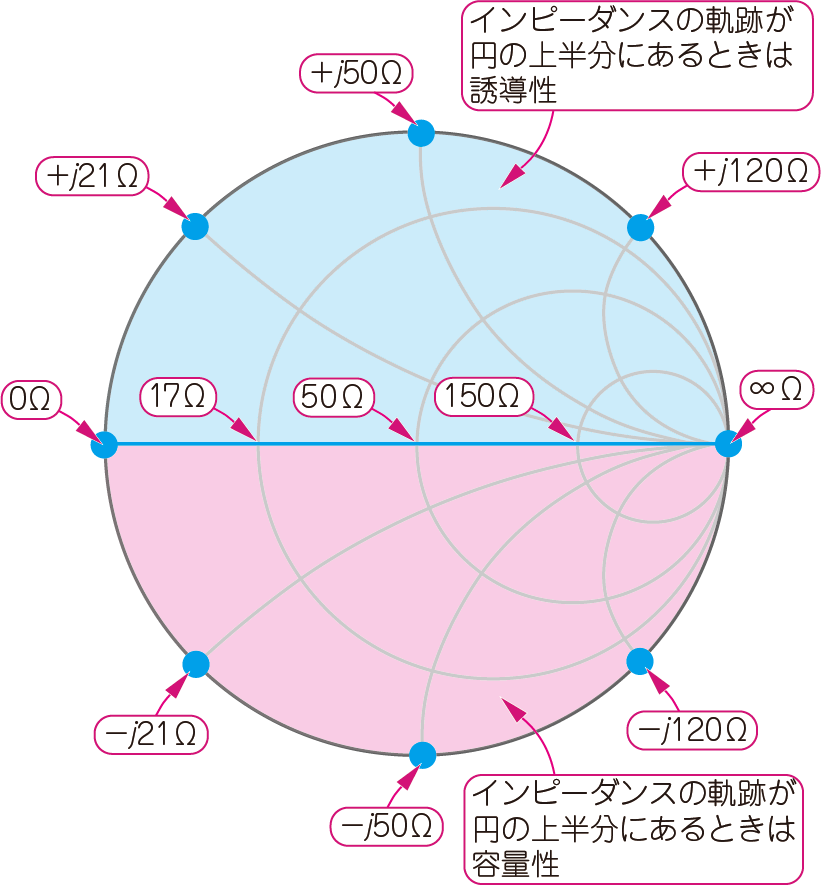
図10に示すのは，スミス・チャートの軸の意味を説明するものです．

抵抗性か？容量性か？誘導性か？

中央の赤色の実線の上にプロットされた場合は，インピーダンスが実数，つまり抵抗性であることを意味します．$50\mathrm{Ω}$で正規化したスミス・チャートでは中心が$50\mathrm{Ω}$，左端は$0\mathrm{Ω}$，右端は$\infty\mathrm{Ω}$です．

赤色の実線の上半分にプロットされる場合は，そのインピーダンスは誘導性(インダクタンス性)で，正の虚数成分をもちます．

赤色の実線の下半分にプロットされる場合は，そのインピーダンスは容量性で，負の虚数成分をもちます．

反射率

本技術連載のVol.2で説明したように，インピーダンスが整合していないと(不整合状態)，反射が起こります．

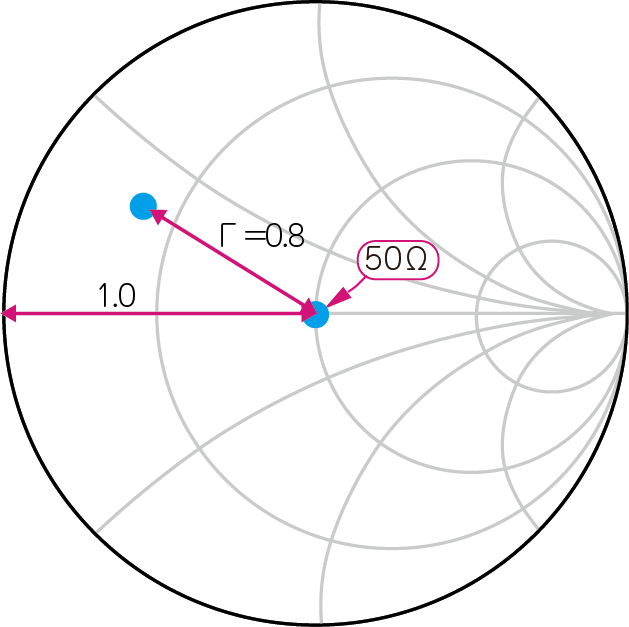
スミス・チャート上のプロット点の中心からの距離は「反射率」は反射の度合いを表しています．図11に例を示します．プロットしたインピーダンスの座標と中心との距離($\it{\Gamma}$，ガンマ)は反射係数を表しています．

電圧定在波比($VSWR$)は，$\it{\Gamma}$ を使って次のように表されます．

\begin{equation} VSWR=\frac{1+\it{\Gamma}}{1-\it{\Gamma}}=\frac{1.8}{0.2}=0.9 \end{equation}

以上のように，スミス・チャートは複素インピーダンスと反射係数を関連付けています．

スミス・チャートを使ってみよう

スミス・チャートを使って，図2～図6のコンデンサやインダクタを追加する前後のインピーダンスの周波数変化を調べると，ゲインが$5\mathrm{GHz}$で最大になった過程や理由が見えてきます．

$\mathrm{AMP}_1$と直列に挿入したコンデンサの効果

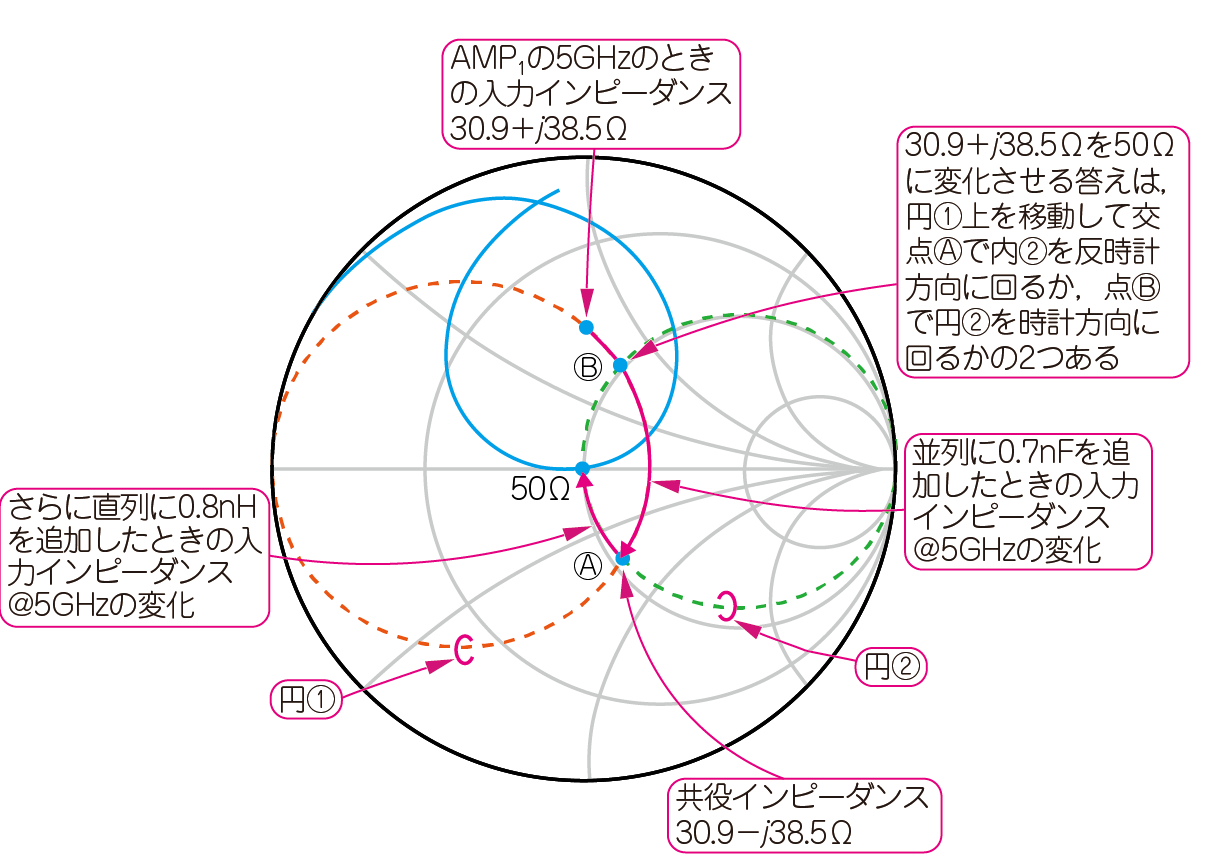
図4の$C_1(0.7 \mathrm{pF}$の効果をスミス・チャートを使って調べてみましょう．

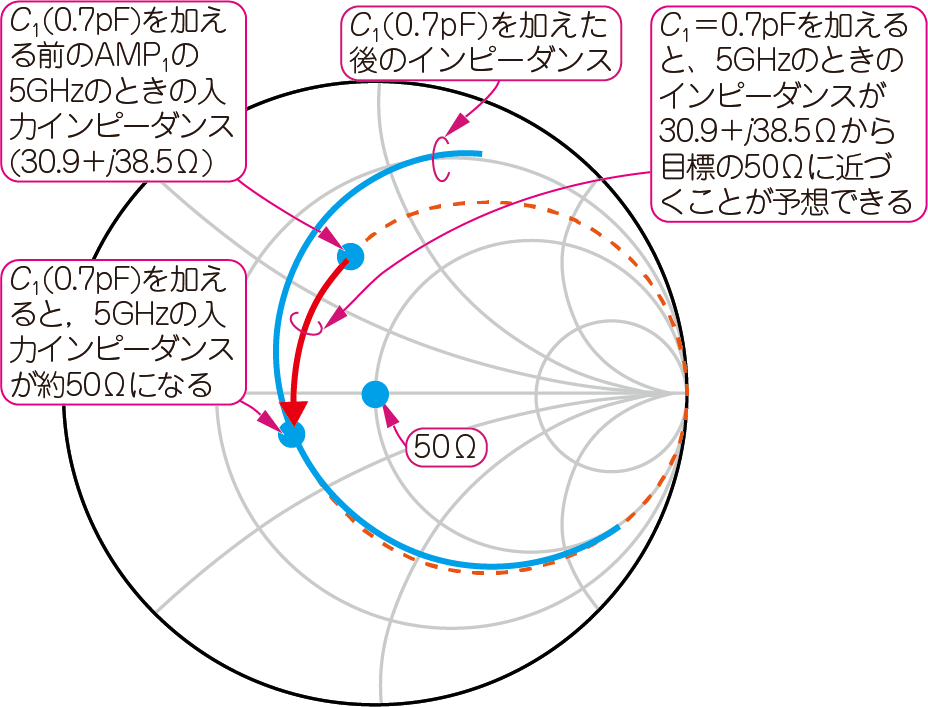
$\mathrm{AMP}_1$の$5\mathrm{GHz}$のときの入力インピーダンスは$30.9+j38.5\mathrm{Ω}$です．$\mathrm{AMP}_1$と直列に容量を接続すると，入力インピーダンス($30.9+j38.5\mathrm{Ω}$)は，$30.9+j38.5\mathrm{Ω}$の点を通る円(右端に接したインピーダンス円)に沿って反時計回りに変化します．容量ではなく，インダクタンスを追加すると，逆に反時計方向に変化します．変化量(奇跡の距離)はインピーダンスによって変わります．

図12に示す青色の実線は，図4の$C_1(0.7\mathrm{pF}$)追加した後のインピーダンスの軌跡です．$5\mathrm{GHz}$のときのインピーダンスは，ピッタリ$50\mathrm{Ω}$ではなく，わずかに容量性にずれています．

この結果から，$C_1$の容量は，$0.7\mathrm{pF}$よりもう少し大きいほうが($0.8 \mathrm{pF}$など)，$50\mathrm{Ω}$に近づきそうだと気づかされます．「$C_1$の値が少々ばらついても，反射係数は変化しなさそうだ」ということもわかります．

$\mathrm{AMP}_1$と並列に追加したインダクタの効果

中心点($50\mathrm{Ω}$)に近づけられる余地が残されているようです．

そこで，$C_1$と信号源との間の信号ラインとグラウンド間に，インダクタ($L_2$)を追加します．

リアクタンスを並列に追加する場合は，スミス・チャートを左右に反転したチャート(アドミタンス・チャートという)の上を移動します．アドミタンス($Y$)とは，インピーダンス($Z$)単位[$\mathrm{Ω}$]の逆数です．いわば信号の流れやすさを表す変数で，単位は[$\mathrm{S}$(シーメンス)]です．

インダクタンスのインピーダンスは，アドミタンス円上を反時計方向に変化します．容量の場合は，その逆(時計方向)に回ります．

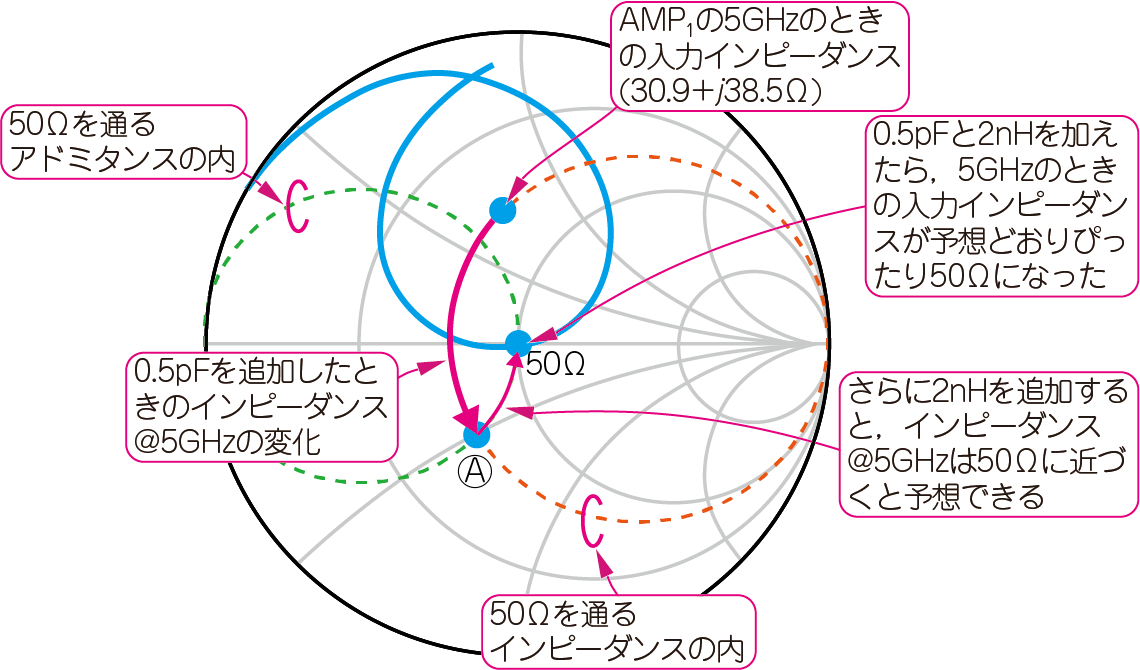
図13を見てください．$\mathrm{AMP}_1$の入力インピーダンス($30.9+j38.5\mathrm{Ω}$)を$50\mathrm{Ω}$に整合させるときには，直列に容量($0.5\mathrm{pF}$)を追加して，$\mathrm{AMP}_1$の入力インピーダンス($Z=30.9+j38.5\mathrm{Ω}$)をインピーダンス円上で変化させ，さらに$50 \mathrm{Ω}$を通るアドミタンス円との交点をピポットにして，インダクタを並列に接続することでそのアドミタンス円上を変化させます．

インピーダンス・マッチングの本質は「共役インピーダンス」を求める作業

図13では，$\mathrm{AMP}_1$の入力インピーダンス($30.9+j38.5\mathrm{Ω}$)からインピーダンスの変化をプロットしました．これは$\mathrm{AMP}_1$の入力回路($\mathrm{P}_2$)から信号源側をみたときのインピーダンスの変化です．

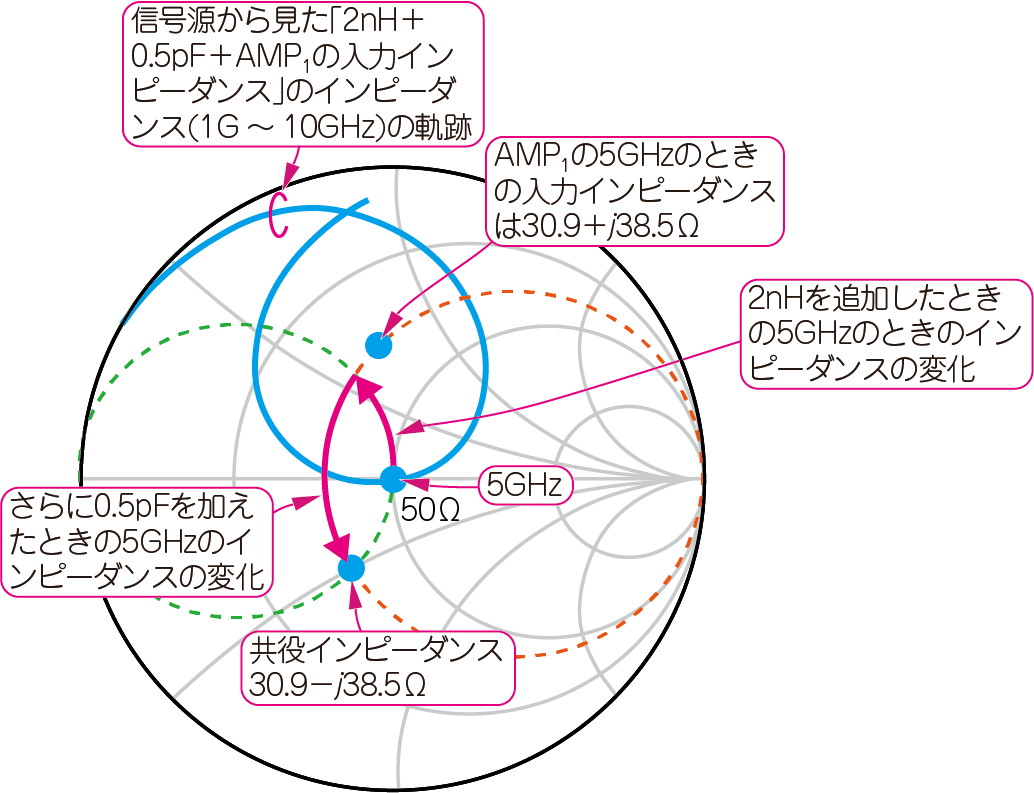
図14に示すのは，逆に，信号源($\mathrm{P}_1$)と並列にインダクタ($2\mathrm{nH}$)を追加，さらに直列に容量($0.5 \mathrm{pF}$)を追加したときのインピーダンスの変化をプロットしたものです．

中心点($50\mathrm{Ω}$)からスタートして，$30.9-j38.5\mathrm{Ω}$でゴールしています．

$\mathrm{AMP}_1$の入力インピーダンスの$30.9+j38.5\mathrm{Ω}$とゴールの$30.9-j38.5\mathrm{Ω}$は，虚数項の極性が逆です．両者の関係を「共役である」といいます．$30.9+j38.5\mathrm{Ω}$は$30.9-j38.5\mathrm{Ω}$の，$30.9-j38.5\mathrm{Ω}$は$30.9+j38.5\mathrm{Ω}$の共役インピーダンスです．

図8では，$\mathrm{X}_1$を入出力インピーダンスが$50\mathrm{Ω}$の理想アンプと仮定しましたが，実際は$45\mathrm{Ω}$かもしれませんし，$j20\mathrm{Ω}$の誘導成分を合わせもっているかもしれません．そんなアンプのマッチング回路を設計するときは，容量成分と誘導成分が打ち消し合う条件を探します．つまり，アンプ側から見たマッチング回路と信号源側から見たマッチング回路のインピーダンスが共役の関係になるように設計します．$50\mathrm{Ω}$にマッチングするのは，説明を簡単にするための1つの事例に過ぎません．

スミス・チャートを使わず計算でマッチングしてみる

スミス・チャートを使わず，計算で整合するとどうなるか実際にやってみましょう．

直列にコンデンサを追加する例

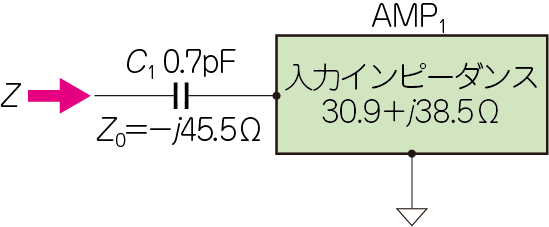
図15に示すように，$\mathrm{AMP}_1$に$0.7\mathrm{pF}$を直接，接続します．これは図4と同じです．

次式から，直列コンデンサ($C_1=0.7\mathrm{pF}$)の$5\mathrm{GHz}$におけるインピーダンス($Z_C$)は，$-j45.5\mathrm{Ω}$です．$Z_C$はリアクタンスなので，複素数の$j$が付きます．

\begin{align} Z_C&=\frac{1}{j2\pi f_C}\\ &=\frac{1}{j2\pi \times 5 \times \ 10^9 \times 0.7 \times 10 ^{-12}}\\ &=-j45.5 \end{align}

次式のとおり，追加後のインピーダンスは，$\mathrm{AMP}_1$の入力インピーダンス($30.9+j38.5\mathrm{Ω}$)に$Z_C$を足して，$Z=30.9-j7.0\mathrm{Ω}$になります．

\begin{align} Z&=30.9+j 38.5-j45.5\\ &=30.9-j7.0 \end{align}

図12で示したように，少し容量性に偏っています．容量を少し大きくすれば，虚数($j$)の項は$0$になると読めます．このくらいのシンプルな回路ならスミス・チャートを使わなくても何とかなりそうです．

直列にコンデンサ，並列にインダクタを追加する例

図16に示すのは，直列にコンデンサ($0.5\mathrm{pF}$)，並列にインダクタ($2\mathrm{nH}$)を追加する例です．これは図6と同じです．計算は一気に煩雑になります．

次に示すのは，コンデンサとインダクタの$5\mathrm{GHz}$におけるインピーダンスです．

\begin{align} Z_C&=\frac{1}{j2\pi f_C}\\ &=\frac{1}{j2\pi \times 5 \times \ 10^9 \times 0.5 \times 10 ^{-12}}\\ &=-j63.7\\ Z_L&=j2 \pi \times 5 \times 10^9 \times 0.5 \times 10^{-12}\\ &=j62.8 \end{align}

$\mathrm{AMP}_1$の入力インピーダンスに，コンデンサを追加したときのインピーダンス$Z_1$と，さらにインダクタを追加したときのインピーダンス $Z_2$は次のとおりです．

\begin{align} Z_1 &= 30.9 + j 38.5 - j 63.7 = 30.9 - j25.2\\ Z_2 &=\frac{ 1}{1/Z_1+1/Z_L}=51.451+j0.193 \end{align}

コンデンサを追加したときのインピーダンスの算出(式(12))までは，図15と同様にシンプルですが，インダクタを追加したときの計算式(式(13)は，とてもに見通しが悪いものになります．

このように，スミス・チャートを使わず，計算式だけで整合条件を探すのはたいへんです．特に整合状態が悪いと，最適な調整方法を見つけることは至難です．これは並列インダクタの定数を変えると，複素インピーダンスの実数項と虚数項がどちらも変化するからです．さらに素子が増えると，対策は絶望的です．

図6の$C$と$L$を入れ替えて低い周波数で整合させてみる

スミス・チャートを使う

改めて図6の整合結果(図7)を見てみると，ピンポイント($5\mathrm{GHz}$}でゲインが最大になっており，そのほかの周波数では大きくゲインが低下しています．これをDC付近から$5\mathrm{GHz}$まで，ゲインが一定のアンプに改造してみます．

図6では，直列に容量($C_1=0.5\mathrm{pF}$)があるため，周波数が低くなるほどゲインは低下します．そこで，コンデンサとインダクタを入れ替えて，低域でもゲインが低下しないようにできないか検討してみます(図17)．

図18に示すのは，図17のインピーダンスの奇跡です．

まず，$\mathrm{AMP}_1$の入力インピーダンス($30.9+j38.5\mathrm{Ω}$)を通るアドミタンス円を描きます．この円は，中心点($50\mathrm{Ω}$)を通るインピーダンス円と2箇所で交差します．どちらの交点を利用しても，整合させることができます．

1つ目は，$\mathrm{AMP}_1$の入力インピーダンス($30.9+j38.5\mathrm{Ω}$)からスタートして円①を移動し，最初の交点(A)を利用して円②に移り，中心点($50\mathrm{Ω}$)に向かう方法です．このインピーダンスの変化は，2つの直列コンデンサで実現できます(図19)．

2つ目は，次の交点(B)を利用する方法です．これは，図17のようにインダクタを直列に追加する必要があります．

2つの選択肢のうちどちらの対策がよいのかは，さまざまな都合によります．最初の交点を利用する1つ目の方法は，容量($C_1$)が小さすぎて実際の部品を選ぶことができません．今回は，直列にインダクタを挿入する2つ目の交点を利用する方法を採用すべきでしょう．

回路シミュレータで計算

上記の2つ目の整合対策を，Qucsというフリーの回路シミュレータで計算してみました．結果を図20に示します．

図20(b)から，$1\mathrm{G}～5\mathrm{GHz}$の広い帯域で，フラットな周波数特性が実現できていることがわかります．

コラム　紙と鉛筆とスミス・チャートでインピーダンス・マッチング

市販のスミス・チャート用紙を買って使ってみてほしい

無料の回路シミュレータやExcelを使えば，スミス・チャートを使わなくても整合条件を見つけることができます．手書きする機会もめっきり減りました．しかし，回路シミュレータでもよいので，欠かさずスミス・チャートを表示させて，インピーダンスの動きを追いかけることは極めて重要です．

スミス・チャートを使って作図する場合は，軌跡の移動量を手計算で求めなければなりません．この方法を簡単に紹介しましょう．

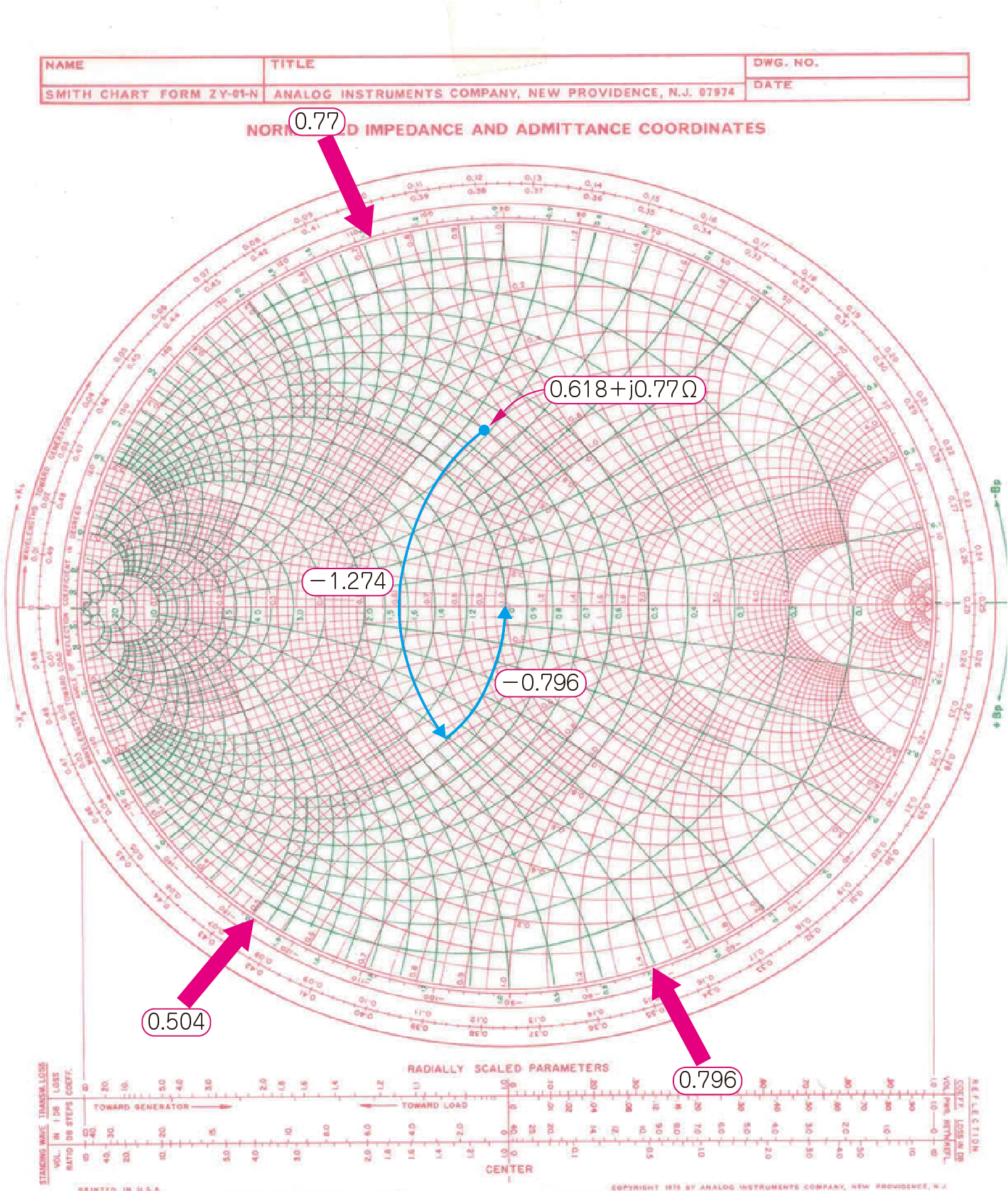
図21に示すのは，市販のイミッタンス・チャート用紙を使って，図13の回路のインピーダンスの変化をプロットしたものです．イミッタンス・チャートとは，インピーダンス＋アドミタンス・チャートを合体させたものです．

正規化を忘れずに

インピーダンスは$50\mathrm{Ω}$で正規化

スミス・チャートは正規化された値が目盛りになっているため，$50\mathrm{Ω}$系では$1.0$が$50\mathrm{Ω}$です．$\mathrm{AMP}_1$の入力インピーダンス($30.9+j38.5\mathrm{Ω}$)は正規化すると，$0.618+j0.77\mathrm{Ω}$になります．

次式の$Z_C$は$50\mathrm{Ω}$で正規化されるため$-1.274$です．

\begin{align} Z_C&=\frac{1}{j2\pi f_C}\\ &=\frac{1}{(j2\pi \times5 \times10^9 \times 0.5 \times 10^{-12}}\\ &=-j63.7 \end{align}

アドミタンスは$0.02\mathrm{S}$で正規化

並列接続のときに利用するアドミタンスは，$1/50=0.02\mathrm{S}$で正規化します． 　次式はインダクタンスのアドミタンスを計算しています．正規化すると$-0.796$です．

\begin{align} Y_L&=\frac{1}j2 \pi f_L\\ &=\frac{1}{j2 \pi \times 5 \times 10^9 \times 2 \times 10^{-9}}\\ &=-j0.016 \end{align}

作図の過程

$0.618+j0.77$を起点とし，インピーダンス円を$-1.274$の距離を反時計方向に回ります．続いて，アドミタンス円を$-0.796$の距離を反時計方向に回ると，中心点($50\mathrm{Ω}$)に到達します．移動量はチャート円の外側にある目盛りを読んで求めます．インピーダンス円は赤色，アドミタンス円は緑色で記されています．

(c)2021 Takashi Kato All Right Reserved.