$V-I$特性を忠実に再現！
SPICEモデル生成ツール Diode SPICE Model Creator

LEDからツェナー，高電圧タイプまで，あらゆるダイオードに対応

著者・講師：善養寺薫/Kaoru Zenyouji（株式会社ディスクリテック）
企画・編集：ZEPエンジニアリング株式会社

自作した理由

従来のモデル生成ツール

PSpiceを始めとする商用SPICEシミュレータの中には，実際のダイオード製品の静特性（$V-I$特性）を入力すると，SPICEモデルを生成してくれる機能を備えたものがあります．

ダイオードのモデリングでは，ショックレーの方程式改良版を用いてSPICEモデルを生成する手法が一般的です．まず測定対象となる実際のダイオードに複数の電圧を加え，対応する電流値を測定します．通常は3パターンの$V-I$データを取得し，それぞれに対応する改良版ショックレー方程式の連立を解くことで，直列抵抗（$R_S$），エミッション係数（$N$），逆方向飽和電流（$I_S$）の3つの変数を求めます．この結果を用いてSPICEモデルを作成することで，理論的には実ダイオードの$V-I$特性を再現できます．しかし，この方法は，実際のダイオード特性と生成モデルの間に差が生じやすく，一致させることは容易ではありません．

実ダイオードの静特性を忠実に再現するモデル生成ツールを自作


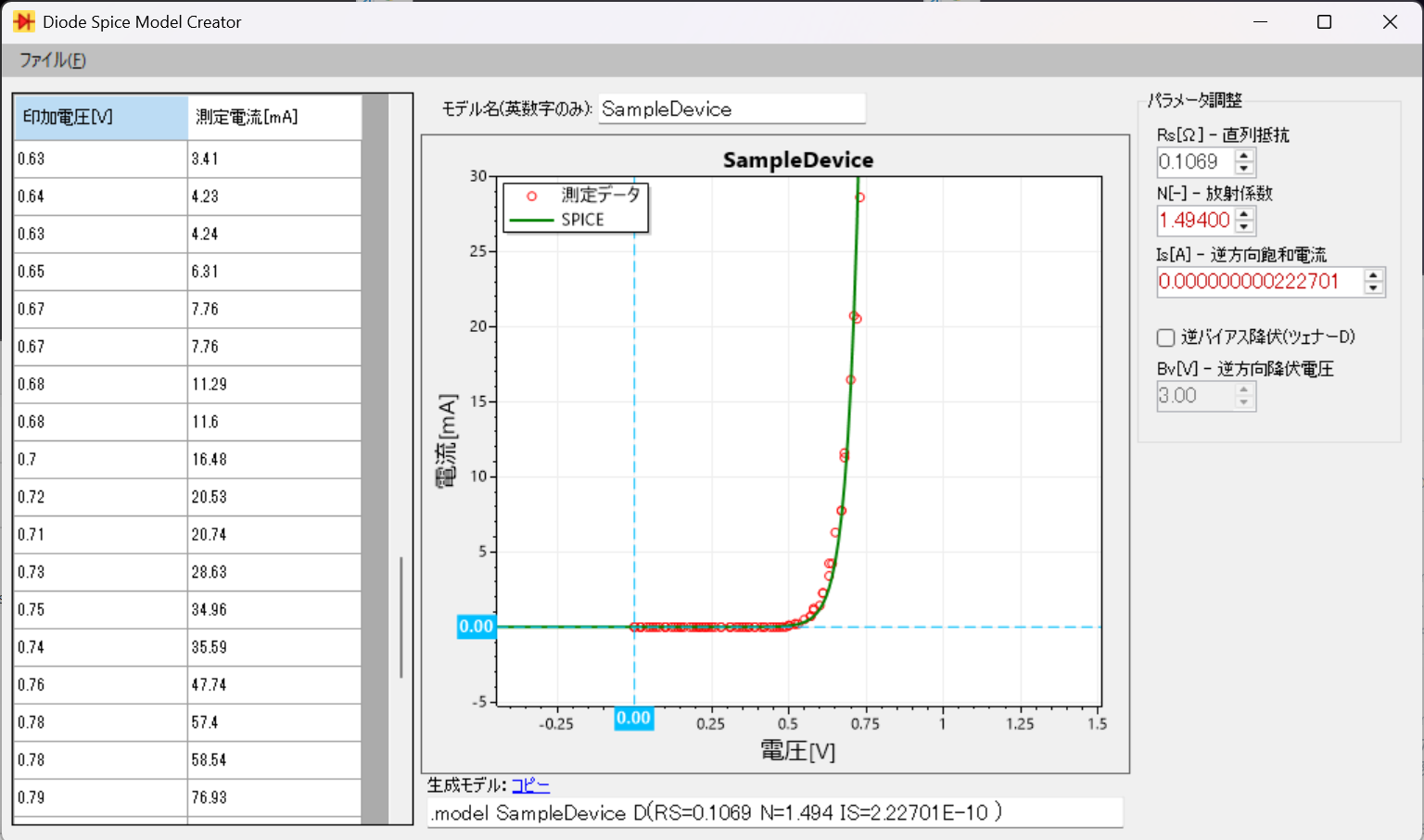
図1　自作のダイオードSPICEモデル生成ツール「Diode SPICE Model Creator」の起動画面（開発：株式会社ディスクリテック）

この課題を解決するために，SPICEモデル生成ツール「Diode SPICE Model Creator」を制作しました．

実ダイオードの$V-I$特性を測定し，グラフとしてプロットします．その上で，ショックレー方程式改良版の3つの変数（$R_S$，$N$，$I_S$）を試行錯誤的に調整し，実ダイオードの$V-I$特性とグラフ形状が一致するまで繰り返します．最終的に一致した時点での方程式を，そのダイオード専用のSPICEモデルとして利用できます．ここで生成されるパラメータの値は，必ずしも実ダイオードの物理的な値と一致するわけではなく，あくまで$V-I$特性の再現性を優先しています．つまり，直列抵抗やエミション係数，飽和電流の値が実物と異なっていても，SPICE上での動作は実際のダイオードと同等にシミュレーションできる点が大きな利点です．

このように，「Diode SPICE Model Creator」は，実運用における特性再現性を第一に考え，測定データに基づいて簡単かつ直感的にSPICEモデルを作成できるツールとして設計されています．これにより，設計者は部品選定や回路解析の精度を高めつつ，試作前のシミュレーションで信頼性の高い回路検証を行うことが可能となります．

Diode SPICE Model Creatorのダウンロード先

本稿で制作したダイオードSPICEモデル生成ツール「Diode SPICE Model Creator」やお試し用のLTspice用回路サンプルが，こちらからダウンロードできます．作成したモデルは，定番の電子回路シミュレータLTspiceで動かすことができます．〈ZEPエンジニアリング〉

実ダイオードの静特性を忠実に再現するSPICEモデル生成ツールを自作

できること

私が制作したモデル生成ツール“Diode SPICE Model Creator”（図1）は，次の3つのパラメータを変更・調整しながら，実際のダイオードと同じ静特性を示すSPICEモデルを作ることができるものです．

LEDはもちろん，$V_F$が数十Vある高電圧ダイオードのモデルも作ることができます．電圧と電流の範囲を狭めることで，厳密なモデルを作ることもできます．逆バイアス時の降伏特性も表現できます．

使い方

STEP1：3つのパラメータを調整する

Diode SPICE Model Creatorを起動すると，初期状態の$V-I$特性グラフが描画されます．右側のパラメータを調整して，ターゲット・ダイオードの$V-I$特性カーブと完全に重なるまで，下記の3つのパラメータを変更・調整します（試行錯誤を繰り返す）．

私は$R_S$は約0.1$\Omega$として，$N$と$I_S$の2つのパラメータを調整しています．

3変数を変更するたびに，Diode SPICE Model Creatorは，最小二乗法を利用して式（1）を解きます．

\begin{equation} \begin{aligned} I_D = - I_S \left( e^{\frac{-B_V + V_D}{V_T}} - 1 + \frac{B_V}{V_T} \right) \end{aligned} \end{equation}

実測値やデータシートのデータを取り込んで，モデリングすることもできます．CSVファイルを読み込む，または，左側の$V-I$入力欄にデータを入れると，赤い丸でグラフ上にプロットされます．CSVのフォーマットのサンプルは，こちらの「サンプルデータ」フォルダから入手可能です．4点以上が入力された場合に，グラフ上に赤い丸が表示されます．

STEP2：生成したモデル・データをSPICEで利用する

3つのパラメータ調整を終えたら，ウィンドウ下側の「生成モデル：コピー」をクリックして，SPICEモデルをコピーします．

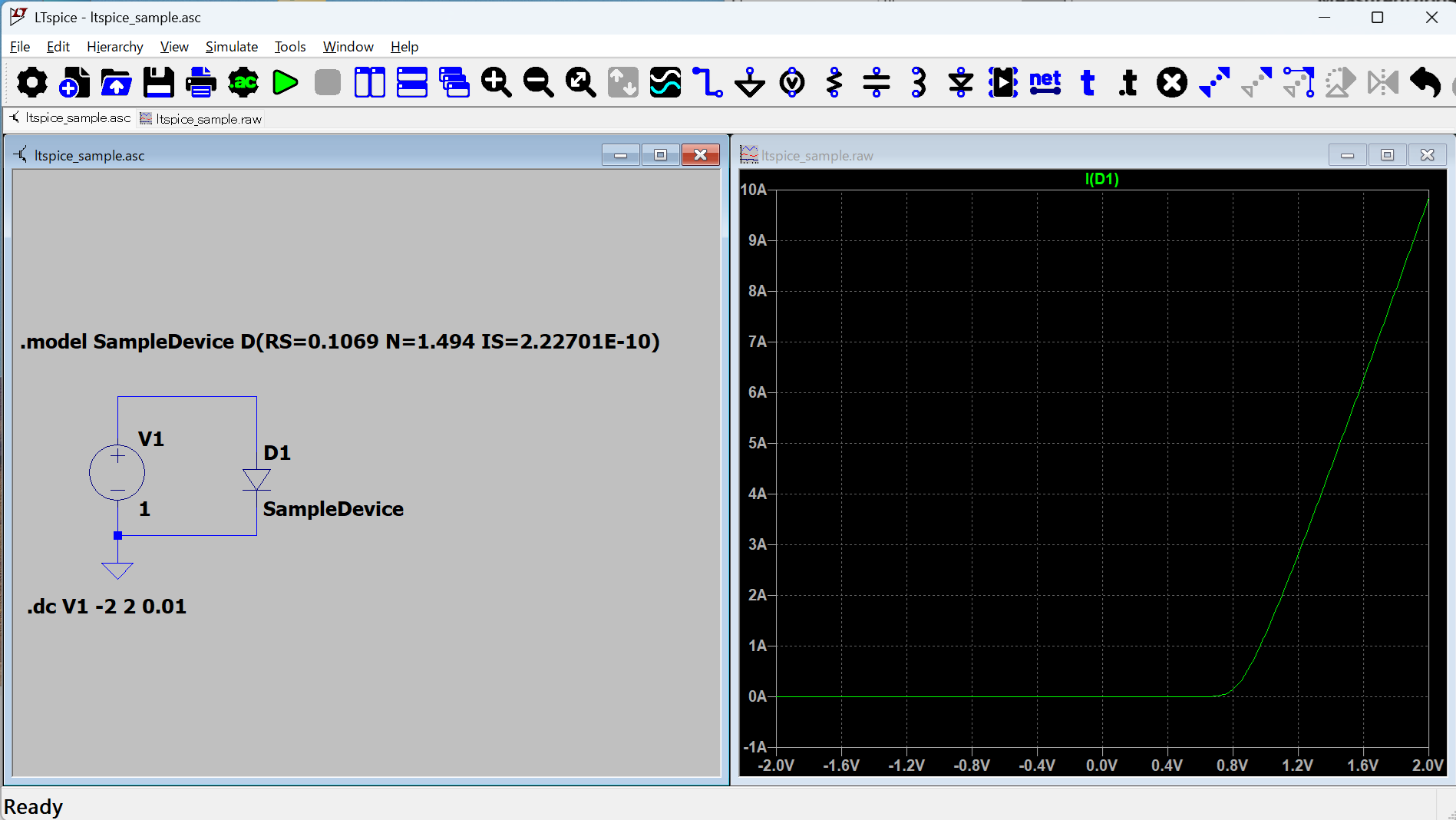
コピーしたデータはそのままSPICEシミュレータで使用できます．例えば，LTspiceの回路図上で［SPICE Directive］（ショートカット・キーは“.”）を選んで，SPICE命令として貼り付けます（図2）．

普段使っているSPICEシミュレータで，生成したモデルを動かしてみてください．パラメータはどんなシミュレータでも使われている基本的なものばかりです．


図2　Diode SPICE Model Creatorで制作したダイオード・モデルを電子回路シミュレータLTspiceで動かしてみた

逆方向のモデリングも可能

Diode SPICE Model Creatorは，逆バイアス印加時のブレークダウン領域のモデリングも可能です．ツェナー・ダイオードなどをモデル化するときは，「□逆バイアス降伏（ツェナーD）」をチェックして，$B_V$パラメータを調整します．

現実のダイオードでは，カソードに正の電圧，アノードに負の電圧を加えると，ある電圧を超えた瞬間，急激に電流が流れ出す逆方向降伏現象が発生します．定電圧源として利用されるツェナー・ダイオードは，この逆方向降伏電圧がコントロールされています．

SPICEではこの逆方向降伏を表すために別のパラメータが用意されています．簡易的には$B_V$というパラメータを設定することで，逆方向降伏をさせることができます．

ダイオードに逆方向バイアス（$-V_D$）を加えて，$-B_V$［V］電圧を下回ると電流（$I_D$）は式（2）に従います．

\begin{equation} \begin{aligned} I_D = I_S \left( e^{\frac{V_D}{N V_T}} - 1 \right) \end{aligned} \end{equation}

逆方向降伏電圧は，$B_V$で指定できると考えてもよいでしょう．逆バイアス時のSPICE計算は厳密には異なります．興味があるかたは調べてみてください．

Diode SPICE Model Creatorでは，$B_V$を設定したときだけ逆方向降伏電圧が現れます．

ここで紹介したモデルは，SPICE上のダイオード・モデルの基本的な部分だけに触れています．温度やノイズ，内部容量に関するパラメータなどがあります．

詳しく知りたい人へ：商用SPICEがダイオード・モデルを求める方法

STEP1：ショックレーのダイオード方程式を変形していく

ショックレー（Shockley）のダイオード方程式から始めます．私は，日本語Wikipedia（ダイオード）に掲載されている方程式を利用しました．

ここで，$I_D$はダイオードのアノードからカソードへ流れる電流，$V_D$はダイオードに加わる電圧（順方向を正），$V_T$は熱電圧と呼ばれる定数で約0.0259V（300K=26.85℃），$I_S$は飽和電流とエミッション係数$N$はダイオードの種類で決まる正の定数です．エミッション係数とは電圧に対して電流がどれだけ急激に増えるかを決める値です．

式（2）のカッコ内を展開すると，式（3）のようになります．

\begin{equation} \begin{aligned} I_D = I_S e^{\frac{V_D}{N V_T}} - I_S \end{aligned} \end{equation}

LTspiceのデフォルト値は$I_S=1 \times 10^{-14}$，通常使う範囲でも$I_S=1 \times 10^{-7}$程度です．非常に小さい値なので省略できます．

そこで，式（3）を式（4）のように書き換えます．

\begin{equation} \begin{aligned} I_D = I_S e^{\frac{V_D}{N V_T}} \end{aligned} \end{equation}

さらに式（5）のように変形します．

\begin{equation} \begin{aligned} \dfrac{I_D}{I_S} = e^{\frac{V_D}{N V_T}} \end{aligned} \end{equation}

すると式（6）が得られます．

\begin{equation} \begin{aligned} V_D = N V_T \ln\left(\frac{I_D}{I_S}\right) \end{aligned} \end{equation}

STEP2：直列抵抗を考慮する

ショックレーのダイオード方程式は，直列抵抗を考慮していません．

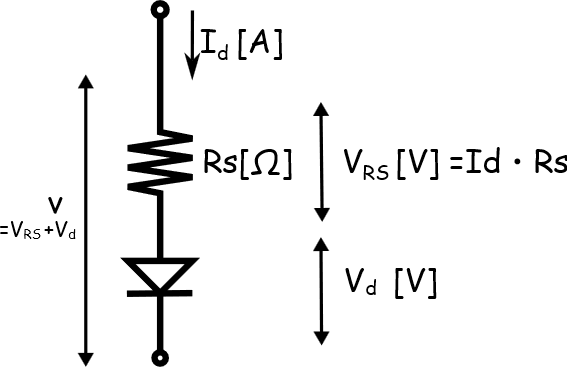
現実のダイオードのふるまいをできるだけ忠実に再現するために，図3のように，直列の直列抵抗を追加します．英語版Wikipediaの「Shockley diode equation」が参考になります．

ダイオード・モデル全体の電圧を$V$，直列抵抗を$R_S［\Omega］$，直列抵抗に加わる電圧を$V_{RS}$，ダイオードに加わる電圧を$V_D$とすると式（7）が得られます．


図3　内部直列抵抗を加えた再現精度の高いダイオード・モデル

\begin{equation} \begin{aligned} V = V_{RS} + V_D \end{aligned} \end{equation}

$V_{RS}=I_D R_S$なので式（8）が得られます．

\begin{equation} \begin{aligned} V = I_D R_S + V_D \end{aligned} \end{equation}

式（8）に式（6）を代入すると，式（9）が得られます．この式は前述の式（1）と同じです．

\begin{equation} \begin{aligned} V = I_D R_S N V_T \ln\left(\dfrac{I_D}{I_S}\right) \end{aligned} \end{equation}

式（9）の各変数の意味は表1のとおりです．

表1　式（9）の変数の意味
変数	意味	モデル・パラメータ
$V_D$	ダイオード・モデルに加わる電圧	既知
$I_D$	ダイオード・モデルに流れる電流	既知
$R_S$	直列抵抗	未知
$N$	エミッション係数	未知
$V_T$	熱電圧（定数：0.0259V@300K）	既知
$I_S$	飽和電流	未知

STEP3：電圧-電流の異なる3連立方程式を解いて，3つの未知数を求める

ダイオードに3パターンの電圧を加えて（$V$），電流（$I_D$）を測って求めます．この電圧と電流の3つの組み合わせを使って，式（9）の3連立方程式を用意して，次の3つの未知数を求めます．

直列抵抗（$R_S$）
エミッション係数（$N$）
飽和電流（$I_S$）

これら3変数が求まったら，次のようにターゲット・ダイオードのモデルのネットリストが得られます（リスト1）．

  
        .model DiodeModelName D(RS=0.1 N=1.752 IS=4E-12)

リスト1　ダイオードSPICEモデルのネットリスト

$V-I$特性を忠実に再現！SPICEモデル生成ツール Diode SPICE Model Creator