商品タイプで探す

Designers' Tips

2026年01月29日号

技術で探す

著者/講師で探す

• 
• 

• 

  

  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 

  

  

  

高周波対応シミュレータ Qucsで学ぶアナログ電子回路 超入門［第2回　目指せ50$\Omega$！高周波のインピーダンス］

GHz×Gbit時代のハードウェアはパソコンで設計する

低周波回路では，各部品を接続するプリント・パターンは，回路図の通りに「部品や回路を単に接続するもの」です．その影響を無視しても，不都合を生じることはほとんどありません．

高周波回路では，プリント・パターンも信号に影響を与える部品として扱う必要があります．その影響を定量的に捉えるためにプリント・パターンの電気的な特性を評価するための「値」が必要です．

第2回では，プリント・パターンの特性値「特性インピーダンス」を紹介します．

「インピーダンス」と「特性インピーダンス」

インピーダンス

電気回路の最初に，電圧，電流と共にインピーダンスを習います．

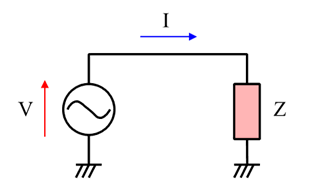
図1に示す回路において，インピーダンス$Z$は式\eqref{eq:impedance}で表され，その値は回路に加わる電圧$V$と，回路を流れる電流$I$の比によって求めることができます．

インピーダンスは複素数で表され，実数部分$R$は抵抗，虚数部分$X$はリアクタンスです．

\begin{align} \label{eq:impedance} Z=\dfrac{V}{I}=R+jX ［\Omega］ \end{align}

低周波回路でも高周波回路でも，インピーダンスはとでも重要なので，少し復習をしておきましょう．

図1の回路が，1個の抵抗$R$，インダクタ$L$，キャパシタ$C$からなる場合，それぞれのインピーダンスは，式\eqref{eq:restance}，式\eqref{eq:inductance}，式\eqref{eq:capacitance}で表されます．

\begin{align} \label{eq:restance} Z=\dfrac{V}{I}=R \end{align}

\begin{align} \label{eq:inductance} Z=\dfrac{V}{I}=j \omega L \end{align}

\begin{align} \label{eq:capacitance} Z=\dfrac{V}{I}=-j \dfrac{1}{\omega C} \end{align}

式\eqref{eq:impedance}，式\eqref{eq:inductance}，式\eqref{eq:capacitance}の“$j$”は虚数単位で，$j^2=-1$であり，位相関係を表しています．

式\eqref{eq:inductance}を変形すると，式\eqref{eq:inductance2}になります．

\begin{align} \label{eq:inductance2} V=j \omega L I \end{align}

インダクタに電圧$V$の信号を加えると，その波は電流$I$より$90^\circ$進むことを表しています．

式\eqref{eq:capacitance}は，式\eqref{eq:capacitance2}のように変形できます．

\begin{align} \label{eq:capacitance2} V=-j \dfrac{I}{\omega C} \end{align}

キャパシタに電圧$V$の信号を加えると，その波は電流$I$よりも$90^\circ$遅れることを表しています．

特性インピーダンス

低周波回路では無視しても問題ないパターンの電気的な影響を定義したものが，特性インピーダンス（characteristic impedance）で，記号“$Z_0$”で表されます．特性インピーダンスは，高周波の伝送線路の特性を表し，伝搬方程式，電信方程式とよばれるものを解いて求められます．

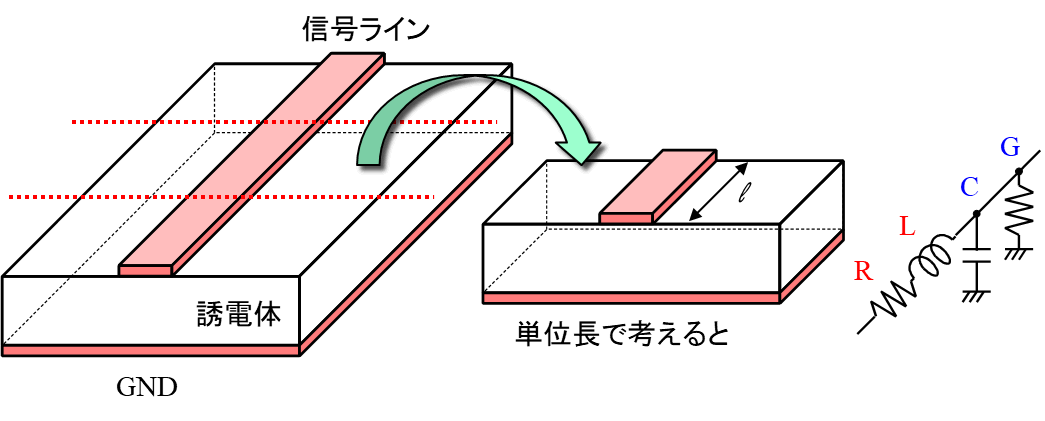
本連載第1回で，プリント・パターンはインダクタンスとキャパシタンスで表されると説明しましたが，導体部分の損失（抵抗，$R$）と誘電体部分の損失（コンダクタンス，$G$）もあります．

伝送線路の等価回路は図2に示す形になります．この伝送線路は，マイクロストリップ・ライン（microstrip line）と呼ばれます．

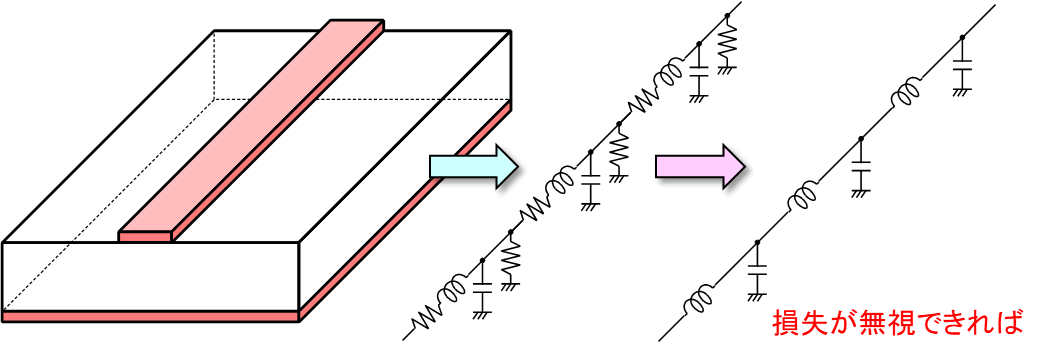
実際の伝送線路は，損失を無視できる微小区間が連続したものなので，等価回路は図3のように表せます．

プリント・パターンのインピーダンス $Z_0$は，単位長さあたりの抵抗を$R$，インダクタンスを$L$，コンダクタンスを$G$，キャパシタンスを$C$とすると，式\eqref{eq:characteristic_impedance1}で表されます．

\begin{align} \label{eq:characteristic_impedance1} Z_0=\sqrt{\dfrac {R+j \omega L}{G+j \omega C}} \end{align}

導体部の損失（$R$）と，誘電体部の損失（$G$）が無視できれば，式\eqref{eq:characteristic_impedance2}に示すようにに簡単化できます．

\begin{align} \label{eq:characteristic_impedance2} Z_0=\sqrt{\dfrac{j \omega L}{j \omega C}} = \sqrt{\dfrac{L}{C}} \end{align}

式\eqref{eq:characteristic_impedance2}で求まる特性インピーダンスは実数で，その単位は[$\Omega$]ですが，単にインダクタンス$L$とキャパシタンス$C$の比から求めたもので，純粋な抵抗ではありません．

伝送線路の長さが変わっても，$L$と$C$の比は変わりません．つまり，特性インピーダンスはその構造で決まり，長さの影響を受けません．

なお上記は「単位長＞幅」の条件下で成立します．

誰でも確実に信号を伝えられるように

高周波信号はつなぐだけでは伝わらない

低周波回路が電圧や電流で信号を伝えるのに対し，高周波回路は電力で信号を伝えます．

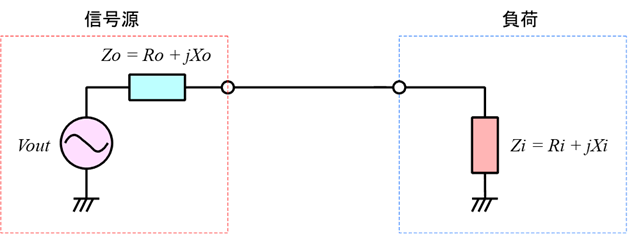
図4において，信号源から負荷へ伝える電力を最大にするためには，式\eqref{eq:matching_1}と式\eqref{eq:matching_2}の2つの条件を満たす必要があります．

\begin{align} \label{eq:matching_1} R_i=R_0 \end{align}

\begin{align} \label{eq:matching_2} X_i=-X_0 \end{align}

この条件が満足されたとき，信号源と負荷が「インピーダンス整合」（impedance matching）され，信号源から負荷に最大電力が供給されます．また，この条件が満足された整合を「共役整合」（conjugate matching）と呼びます．

基準インピーダンスを決めておけば安心

複数の回路を接続する場合，つなぎ合わされる回路間で共役整合条件を満足させるのは大変な作業です．また，回路どうしをプリント・パターンやケーブルで接続するときは，プリント・パターンやケーブルを「特性インピーダンスをもつ回路と考えて，共役整合させます．

もっと簡単に回路どうしを接続するにはどうしたらよいのか？ヒントは式\eqref{eq:matching_1}と式\eqref{eq:matching_2}です．

最初から各回路の入出力インピーダンスのリアクタンス成分を0にしておき，抵抗成分が同じ値になるように設計しておくと何も考えずに接続できます．つまり，基準となるインピーダンスを決めて，それに合わせて回路を設計します．さらに，プリント・パターンやケーブルの特性インピーダンスも基準インピーダンスに合わせればいいのです．

50Ωが都合がいい

高周波回路では通常，50$\Omega$が基準のインピーダンスとなっています（一部，放送機器関係では75$\Omega$も使われる）．

なぜ，50$\Omega$なのか？諸説ありますが，私なりに次のような点で（主に物理的な寸法の理由で），50$\Omega$が最適な基準インピーダンスだと感じています．

マイクロストリップ・ラインの現実的な特性インピーダンスの範囲は，20 $\sim120\Omega$で，上下限の相乗平均は式\eqref{eq:refimpedance_2}です．同軸ケーブルの外部導体と内部導体の直径も扱いやすい寸法になります．

\begin{align} \label{eq:refimpedance_2} \sqrt{20 \times 120}= 49 \Omega \fallingdotseq 50\Omega \end{align}

マイクロストリップ線路の特性インピーダンスを求めてみた

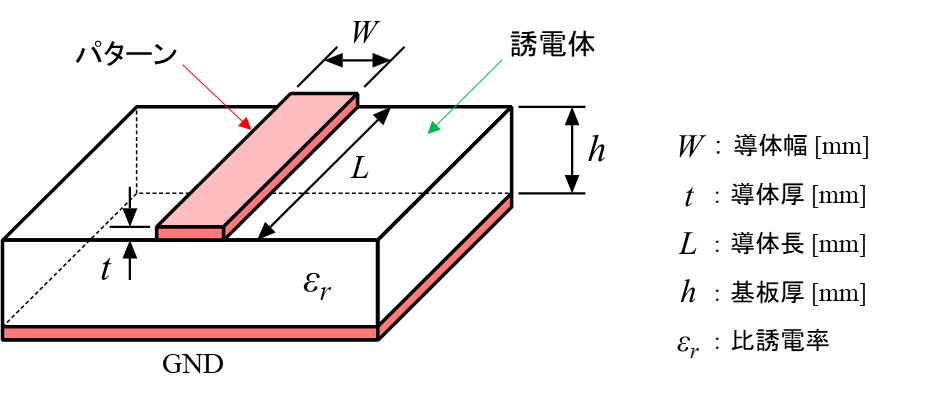
図5に示すのは，高周波回路や高速ディジタル基板で利用されている定番の伝送線路「マイクロストリップ線路」です．

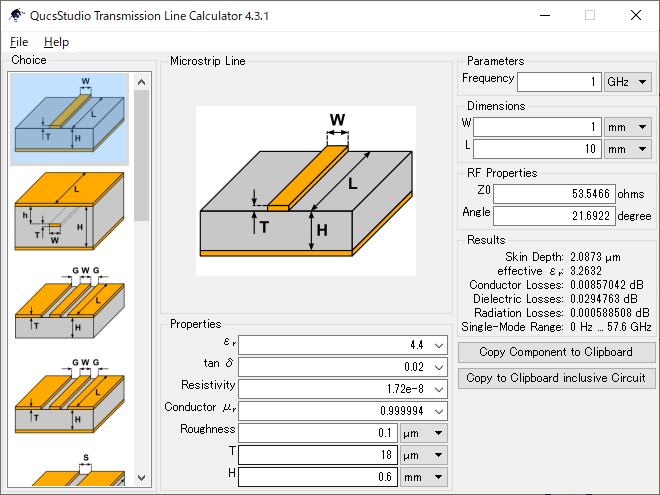
QucsStudioに付属する伝送線路計算ツールを使って，図2のマイクロストリップ線路（FR-4，$W=1$mm，$L=10$mm，$h=0.6$mm，$t=18\mu$m）の特性インピーダンスを求めてみましょう．

計算ツールに基材の基本特性である誘電率や，物理寸法を入力すると，特性インピーダンス$Z_0$が表示されます．

図6に示すとおり，結果は“$Z_0=53.55\Omega$”で約50$\Omega$です．

コラム　Z0=53.55Ωの伝送線路は許容できる？

高周波信号は特性インピーダンスの変化点で反射する

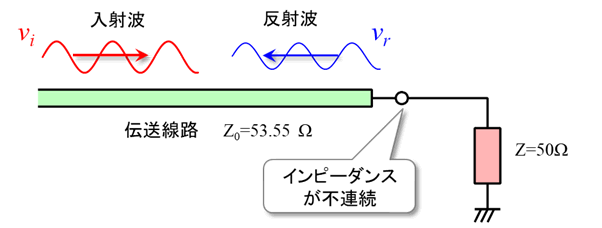
図6の計算結果は53.55$\Omega$で，基準インピーダンス50$\Omega$から少しずれています．

図7に示すように，特性インピーダンス53.55$\Omega$のプリント・パターンと50$\Omega$の回路と接続すると，インピーダンスが不連続になる接続点で反射が発生して，信号が信号源にもどっていきます．入力した電力の一部が入力側に戻されてしまうわけです．

プリント・パターン上には，入射波と反射波が足し合わされた「定在波」と呼ばれる波を生じます．定在波の振幅は，元の入射波の振幅よりも大きくなるので，電磁波の空間への放射も大きくなります．

反射を表す3つの指標

反射には，反射係数$\Gamma$，電圧定在波比 $VSWR$（Voltage Standing Wave Ratio），リターン・ロス$RL$の3つの表し方があります．反射係数$\Gamma$が最も基本となる表し方ですが，回路の仕様や反射特性データを表す場合は，電圧定在波比$VSWR$やリターンロスが使われます．

その1：反射係数 \Gamma

反射係数$\Gamma$は，入射波と反射波の比で求められ，反射の大きさと入射波と反射波の位相関係を表します．入射波と反射波を直接測定して求めることはできませんが，接続される2つのインピーダンスを使って，式\eqref{eq:gamma_1}から簡単に求められます．図7の条件で計算すると次のようになります．

\begin{align} \label{eq:gamma_1} \Gamma&=\dfrac{Z-Z_0}{Z+Z_0} \\ &=\dfrac{50-53.55}{50+53.55}=\dfrac{-3.55}{103.55}=-0.034=0.034 \angle 180^\circ \end{align}

その2：電圧定在波比 VSWR

$VSWR$は，図7の伝送線路上に存在する電圧定在波の，最大振幅と最小振幅の比を表したものです．入射波と反射波の位相が同相となったポイントで，定在波の振幅は最大になります．

入射波と反射波の位相が逆相になったポイントで，定在波の振幅は最小になります．定在波の最大振幅と最小振幅を直接測定して求めることはできませんが，反射係数の値（大きさ）を使って，式\eqref{eq:vswr_1}から求めることができます．

\begin{align} \label{eq:vswr_1} VSWR&=\dfrac{1+|\Gamma|}{1-|\Gamma|} \\ &=\dfrac{1+0.034}{1-0.034}=1.034/0.966=1.070 \end{align}

その3：リターン・ロス RL

リターン・ロスは，入射電力と反射電力の比を［dB］で表したものです．つまり，入射電力に対して反射電力が何dB減衰しているかを表しています．

リターン・ロスも反射係数の値（大きさ）を使って，式\eqref{eq:returnloss_1}で求めることができます．

\begin{align} \label{eq:returnloss_1} RL&=-20 \log|\Gamma| \\ &=-20\log 0.034 =29.37 \text{［dB］} \end{align}

伝送線路やケーブルを含めた受動回路に要求される反射特性は，$|\Gamma|\leq 0.1$です．他の表し方では，$VSWR\leq1.22$，$RL\geq20$dBです．

$|\Gamma| = 0.1$ は，反射電力では1$\%$です．反射電力が1$\%$以下であれば，反射が無いとみなしても問題ないレベルです．上記の例では，反射電力は約0.12$\%$なので，反射特性としてまったく問題ないレベルです．

まとめ：特性インピーダンスは伝送線路の電気的なふるまいを表すもの

今回は，インピーダンスの復習から始まって，特性インピーダンス，基準インピーダンスを見てきました．次回は，式\eqref{eq:characteristic_impedance2}に，第1回で求めたパターンのインダクタンスとキャパシタンスを適用し，特性インピーダンスを求めてみましょう．

参考文献

1. 市川 裕一（I-laboratory）、高周波回路の設計と製作、誠文堂新光社。
2. 市川 裕一（I-laboratory）、はじめての高周波測定、CQ出版株式会社。
3. 市川 裕一（I-laboratory）、復刻版 GHz時代の高周波回路設計【オンデマンド版】、CQ出版株式会社。
4. 加藤 隆志（株式会社ラジアン）、5G時代の先進ミリ波ディジタル無線実験室、ZEPエンジニアリング株式会社。
5. 知念 幸勇、［VOD/KIT］3GHzネットアナ付き！RF回路シミュレーション＆設計・測定入門、ZEPエンジニアリング株式会社。
6. 川口 正、［VOD/KIT］ポケット・スペアナで手軽に！基板と回路のEMCノイズ対策 10の定石、ZEPエンジニアリング株式会社。
7. 池田 浩昭、［Webinar/Book/data］電磁界シミュレーションによるプリント基板設計&EMC対策、ZEPエンジニアリング株式会社。

---

« ZEPマガジン前の記事「高周波対応シミュレータ Qucsで学ぶアナログ電子回路 超入門［第1回　プリント・パターンは$L$と$C$でできている］」

ZEPマガジン次の記事「計測のための24ビット$\Sigma\Delta$型A-Dコンバータ活用［第1回　高分解能$\times$高$SNR$の鍵「ノイズ・シェーピング」］」 »