商品タイプで探す

Designers' Tips

2026年01月29日号

技術で探す

著者/講師で探す

• 
• 

• 

  

  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 

  

  

  

計測のための24ビット$\Sigma\Delta$型A-Dコンバータ活用［第1回　高分解能$\times$高$SNR$の鍵「ノイズ・シェーピング」］

16～32 ビットの超高精度ディジタル値を得るために

• ［著］石井 聡 / Satoru Ishii / アナログ・デバイセズ
• ［協力］DigiKey
• ［編集］ZEPエンジニアリング

　　【Index】

• 第1回：高分解能$\times$高$SNR$の鍵「ノイズ・シェーピング」
• 第2回：実験研究！市販ICの内蔵ノイズ・シェーピング回路］
• 第3回：低ノイズA-D変換システムの設計

計測分野で注目される24ビット$\Sigma\Delta$（シグマ・デルタ）型A-Dコンバータは，高分解能かつ高信号対雑音比（$SNR$）を実現する技術として重要です．その中核技術が「ノイズ・シェーピング（noise shaping）」です．本稿では，このノイズ・シェーピング技術を複数の観点からわかりやすく解説します．

$\Sigma\Delta$型ADCは，1ビット出力の変調器と，後段のディジタル・フィルタと間引き回路から構成されており，16～32ビットの高分解能レンジ用です．特にセンサ信号の精密検出に適しています．

$\Sigma\Delta$変調器は，入力信号と出力から帰還された1ビットDACの出力電圧を引き算して，積分器を経て，コンパレータで2値化（量子化）し，出力ビットが得られます．この量子化の過程で発生する量子化ノイズのエネルギを高周波数側に押しやる$\Sigma\Delta$変調器の処理「ノイズ・シェーピング」が分解能向上の鍵です．

後段のディジタル・フィルタは，シリアル化された1ビット・データを多ビット精度に変換し，ロー・パス・フィルタ処理で量子化ノイズの高周波成分を除去します．これにより，16～32ビット相当の高精度ディジタル値が得られ，間引き処理で更新速度が決まります．

ノイズ・シェーピングの動作は，入力電圧に応じたシリアル・ビット列の平均値が入力電圧の大きさに比例し，量子化ノイズが高周波に押しやられていることがスペクトル解析で確認できます．数式的には，信号成分は$\Sigma\Delta$変調器の入出力で素通しで伝達されます．一方量子化ノイズは，微分回路的な動作特性により，低周波のノイズ成分が高周波に押しやられるというしくみになっています．

本稿の内容は，電子回路設計者や計測技術者，大学・大学院の学生に最適で，ノイズ・シェーピングの基礎理解と応用展開に役立つでしょう．〈著：ZEPマガジン〉

1．はじめに

本稿では，高分解能を可能にするA-D（Analog-to-Digital）コンバータ（本稿では以降「ADC」と呼ぶ）である，$\Sigma\Delta$（シグマ・デルタ）型ADCの「ノイズ・シェーピング技術」について，複数の視点からそのしくみを解きほどいてみます．

$\Sigma\Delta$型ADCは1ビット・データ出力（シリアル・ビット列）を基本として動作しているにもかかわらず，なぜ高い分解能と$SNR$（Signal to Noise Ratio；信号対ノイズ比）が実現できるのか納得できるでしょう．なおこの方式を「ΔΣ方式」と呼ぶ場合もありますが，アナログ・デバイセズでは「$\Sigma\Delta$方式」と呼んでいます．実際はどちらも同じものです．

2．高分解能を実現する$\Sigma\Delta$技術の基本的なしくみ

一般的に$\Sigma\Delta$型ADCは分解能が高く，16ビットから32ビットの高分解能レンジを担当します．そのためセンサの信号検出などに最適といえます．

前段は$\Sigma\Delta$変調器，後段はディジタル・フィルタと間引き

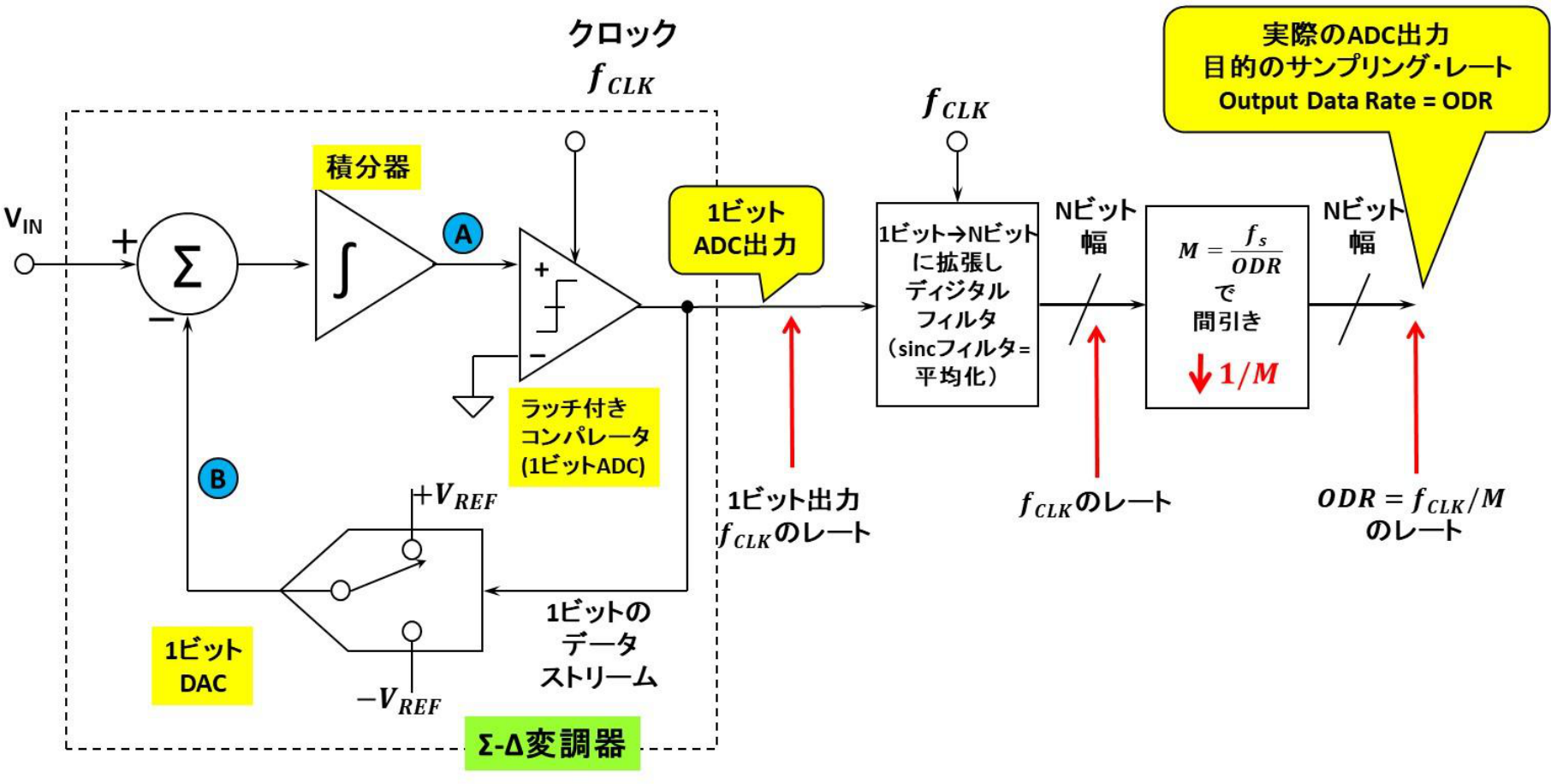
図1に$\Sigma\Delta$型ADCのブロック図を示します．前段が$\Sigma\Delta$変調器，後段がディジタル・フィルタと間引き（ディジタル回路）から成り立っています．$\Sigma\Delta$変調器は入力をコンパレータで2値化するので，「1ビットのADC」と考えられます．次回に$\Sigma\Delta$ ADCの動きをデモするため用いるアナログ・デバイセズのAD7401は，この$\Sigma\Delta$変調器の部分だけに相当し，図中後段のディジタル・フィルタと間引きは，AD7401の後段に別置するFPGA（Field Programmable Gate Array）などで処理します．

本稿では一番基本的な，帰還回路が1経路となる「1次」の$\Sigma\Delta$変調器を解説します．AD7401の$\Sigma\Delta$変調器は2次構成ですが，4次，5次など高次の帰還経路をもった$\Sigma\Delta$変調器も高性能な$\Sigma\Delta$型ADCでは用いられています．とはいえ基本的には1次の構成を理解できれば十分です．

1次$\Sigma\Delta$変調器の構成

1次$\Sigma\Delta$変調器は入力アナログ電圧（入力信号）が，帰還経路からの1ビットD-Aコンバータ（本稿では以降「DAC」と呼ぶ）の電圧と引き算されます．それが積分器を経由して，コンパレータで2値化され，1ビット・データ（1ビット情報）としてラッチされ，$\Sigma\Delta$変調器からディジタル情報として出力される構成になっています．

またこのラッチされた1ビット・データ（$\Sigma\Delta$変調器出力）は帰還経路にもフィードバックされ，さきの1ビットDACの出力電圧設定情報になります．この構造により，サンプリングで発生する量子化誤差電圧（量子化ノイズ．詳しくは後述）のエネルギを「高い周波数に押しやる」という動作を実現できます．これを「ノイズ・シェーピング」といいます（日本語でいうと，「雑音整形/雑音成形」）．本稿ではこのうごきを詳しく述べていきます．

後段のディジタル・フィルタによる量子化ノイズ低減

任意の入力アナログ電圧レベルにおいて，1ビットのADCと考えられる$\Sigma\Delta$変調器から1回のサンプリングで得られた，1ビット・データはほとんど意味をもちません．多数のサンプル値を平均したときこそ，その値が意味をもちます．

図1のように，後段のディジタル・フィルタによりLPF（Low Pass Filter）処理を行い，ノイズ・シェーピングで高い周波数に押しやられた余分な量子化ノイズ成分を除去します．

このディジタルLPFには2値の1ビット・シリアル・データ列が入力されます．目的の分解能が24ビットであれば，この2値の1ビットを24ビット以上にビット幅に広げて（ビット拡張して），そのビット幅精度でディジタル・フィルタ演算します．ディジタルLPFで24ビットの分解能を作り込むわけです．

その結果，入力アナログ電圧量が目的の24ビット分解能のディジタル値（A-D変換された値）として得られるようになります．さらにこの結果は「間引き処理」され，サンプリング・クロック周波数より遅い更新速度で（設定によって異なるが，たとえば16, 128, 1024サンプルに1回などで）出力します．間引き処理を「デシメーション」ともいいます．

このように$\Sigma\Delta$型ADCは「高速なサンプリング・クロック＋ $\Sigma\Delta$変調動作」が1つめの肝（キモ），もう1つの肝がその後段の「ディジタルLPFとデシメーション」なのです．このディジタルLPFとデシメーションについては，次回もう少し詳しく説明します．

3．1次$\Sigma\Delta$変調器のノイズ・シェーピングのしくみをそのうごきから理解する

$\Sigma\Delta$変調器はサンプリング・クロック周波数$f_{CLK}$のレートで$\Sigma\Delta$変調動作をおこないます．

$\Sigma\Delta$変調器は2値（H/Lに相当するディジタル値）の出力しかない1ビットのADCです．1回のサンプリングで得られた2値のディジタル値（ここではHをリファレンス電圧$+V_{ref}$ [V]，Lを0 Vと考える）と入力アナログ電圧量との差が量子化誤差電圧になります．これが量子化ノイズです．ノイズ・シェーピングはこの量子化ノイズのエネルギを，高い周波数側に押しやるように動作するものです．

そういう私もノイズ・シェーピングの解説を30年以上前に，とある技術雑誌で見たとき，なんど読んでも理解できませんでした（多分筆者自体が理解していなかったと思われる…）．そんなトラウマから，本稿（今回と次回）ではこのノイズ・シェーピングを「複数の視点から」わかりやすく解説していきたいと思います．

実際にシミュレーションで$\Sigma\Delta$変調器の動作を確認

それでは実際にノイズ・シェーピングが動作するようすをLTspiceのシミュレーションで確認してみます．ここではリファレンス電圧を2 V，サンプリング・クロック周波数を1 kHzとして，16回サンプリング・クロックが入り（$\Sigma\Delta$変調が行われ），16個のシリアル・ビット列が得られるものとします．

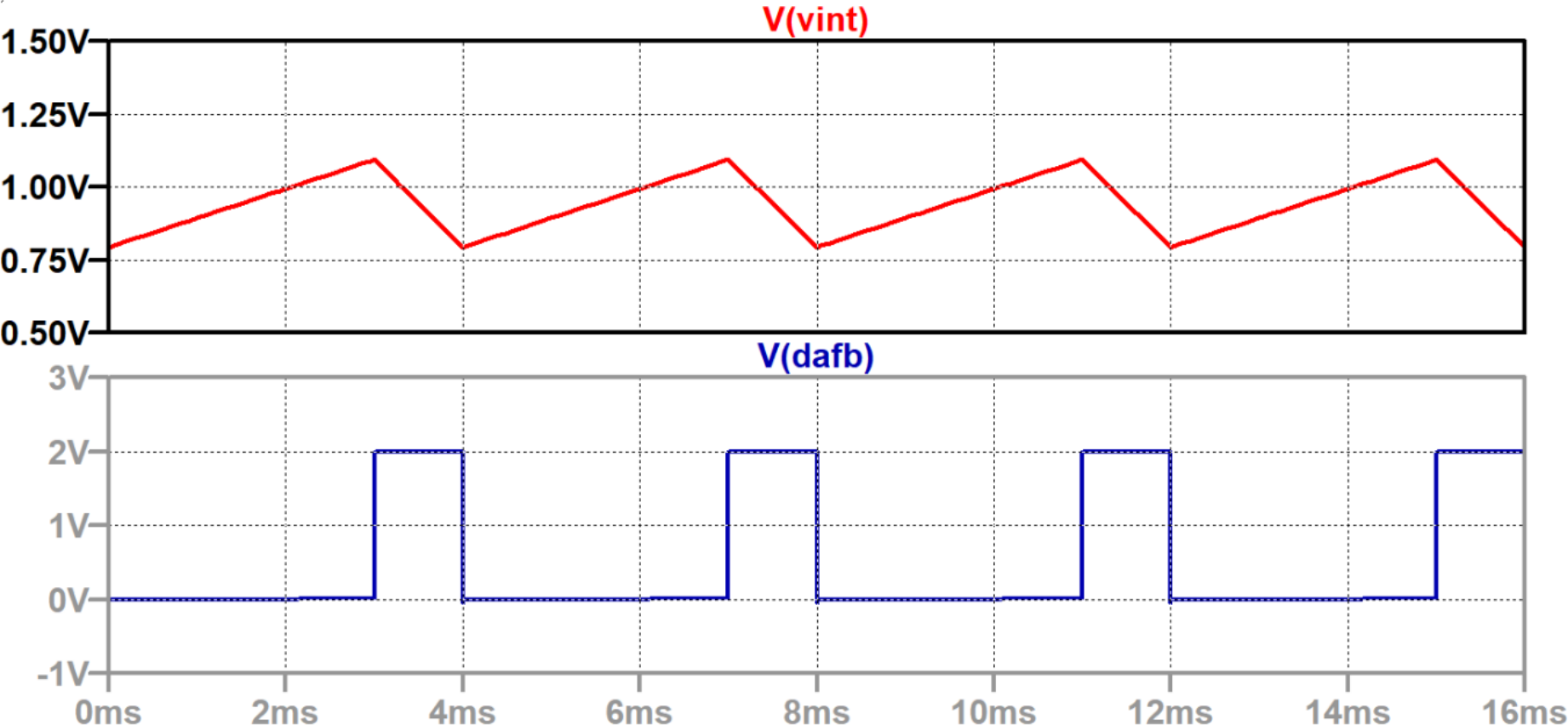
図2に示すのは，入力電圧が0.50 V（リファレンス電圧の1/4）のときの$\Sigma\Delta$変調器の動作です．

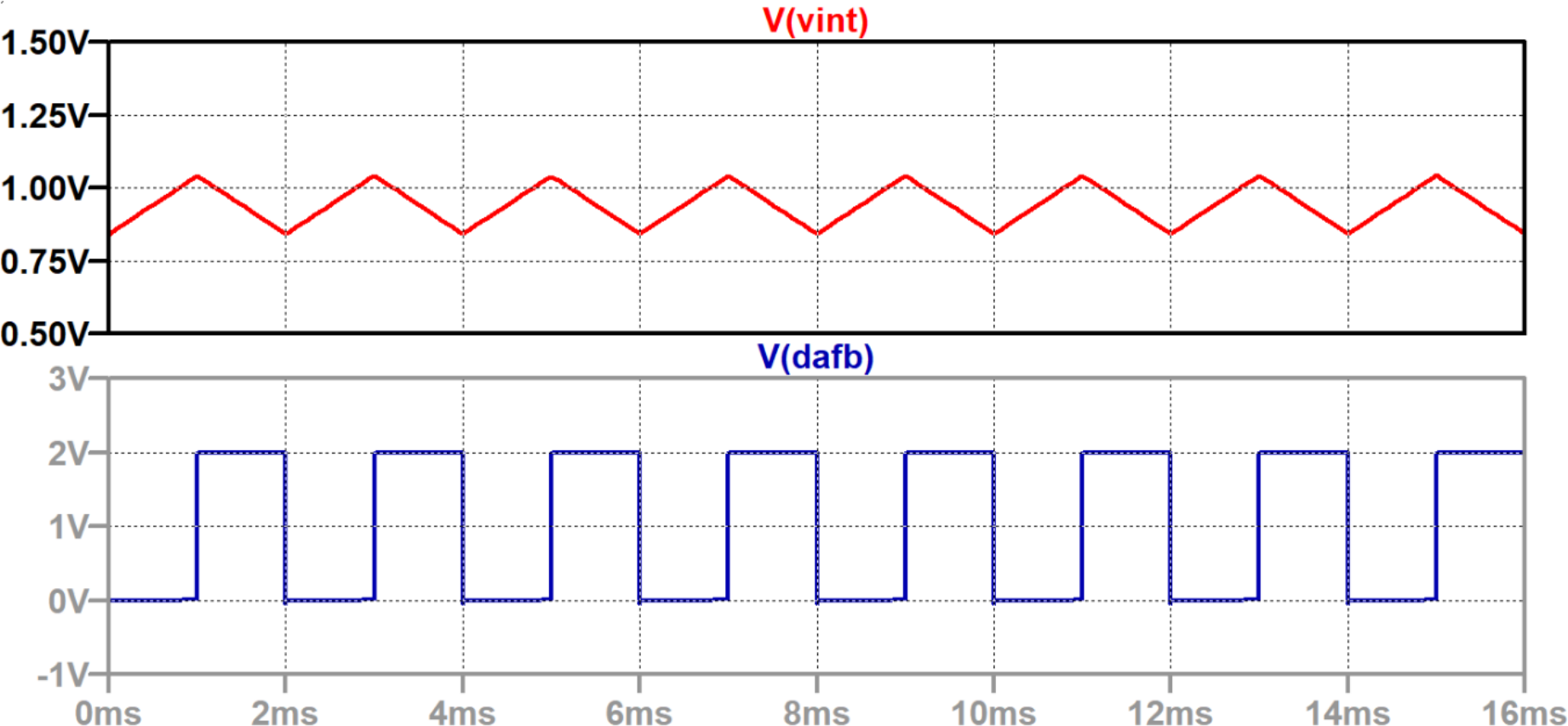
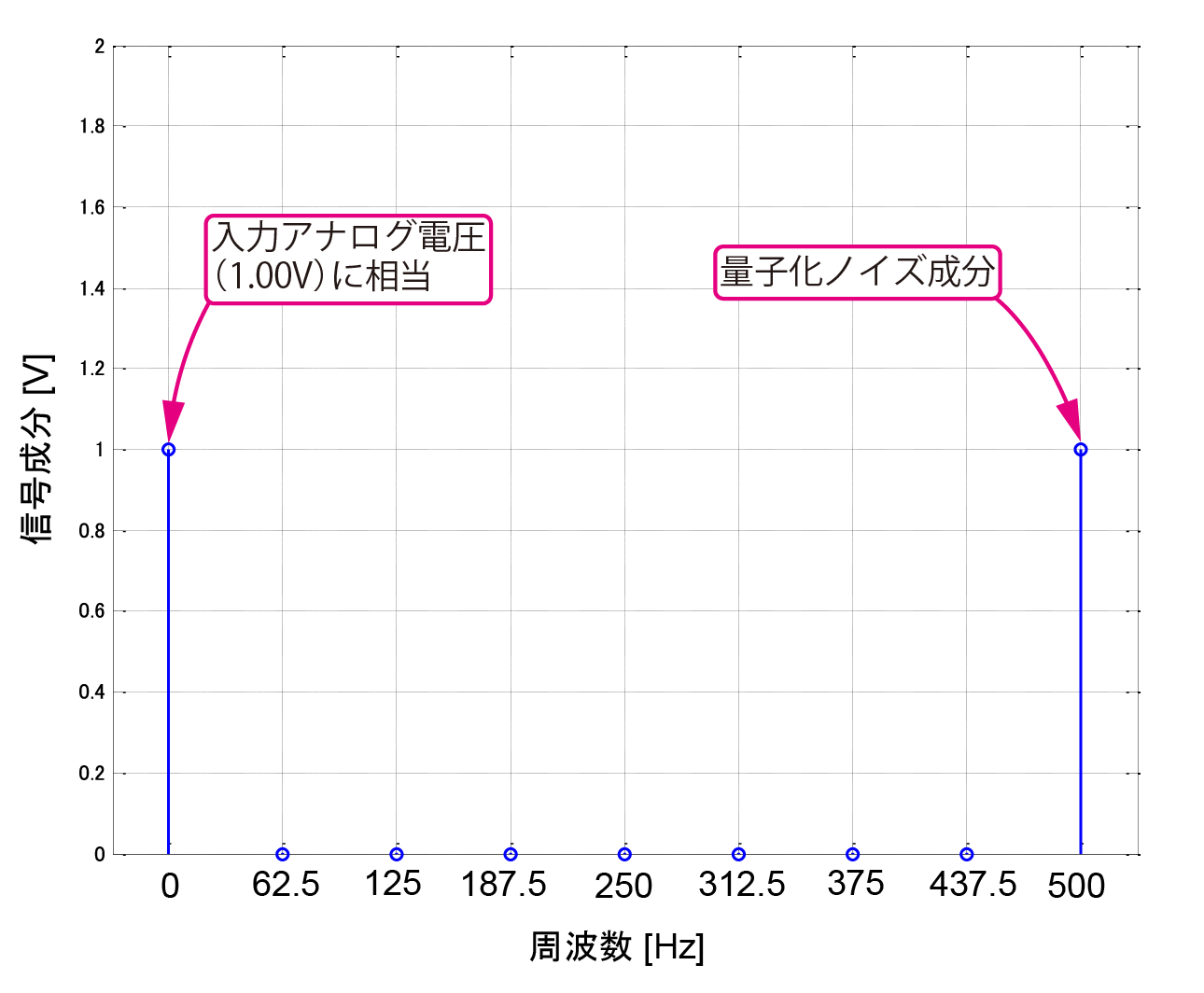
図3に示すのは，入力電圧が1.00 V（リファレンス電圧の1/2）のときの$\Sigma\Delta$変調器の動作です．

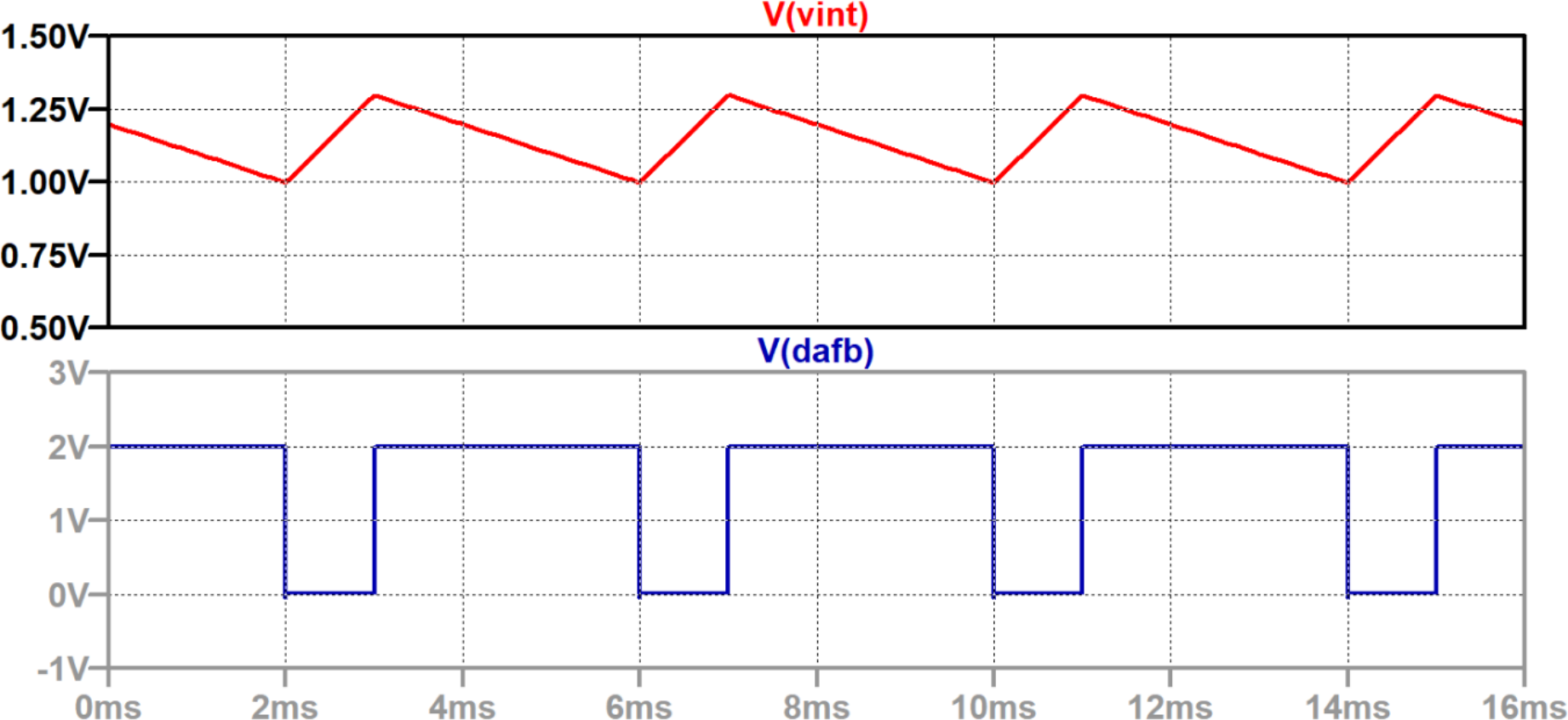
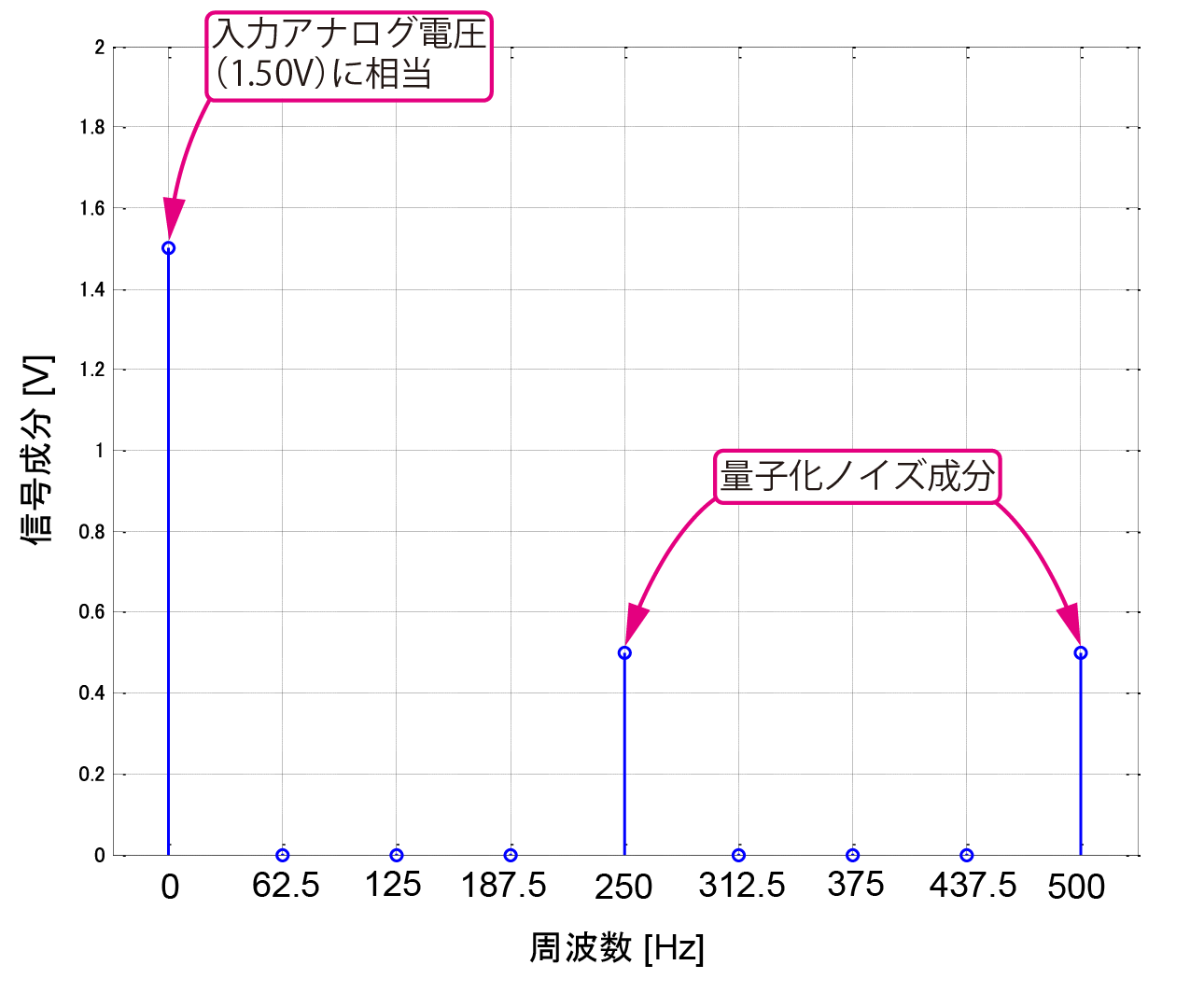
図4に示すのは，入力電圧が1.50 V（リファレンス電圧の3/4）のときの$\Sigma\Delta$変調器の動作です．

それぞれ上が積分器出力，下がシリアル・ビット列です．

Hをリファレンス電圧$+V_{ref}$ [V]，Lを0 Vとし，この16個のシリアル・ビット列の「平均値」を計算してみると，入力電圧の大きさになります．

入力電圧がリファレンス電圧$+V_{ref}$（ここでは2 V）に近い場合，シリアル・ビット列内のHの数はLの数より多くなっています．

ビット列を周波数スペクトルで考えると高い周波数の方にノイズが押しやられている

得られた16個のシリアル・ビット列は，状態が変化しています．この16ビット列を「信号電圧」として考えると，予想されることとして，この16ビット列の周波数スペクトルは，

1. 広い周波数範囲に広がっており，
2. それも高い周波数成分が存在し，
3. 直流成分が入力アナログ電圧に相当する

これを実際に見てみましょう．

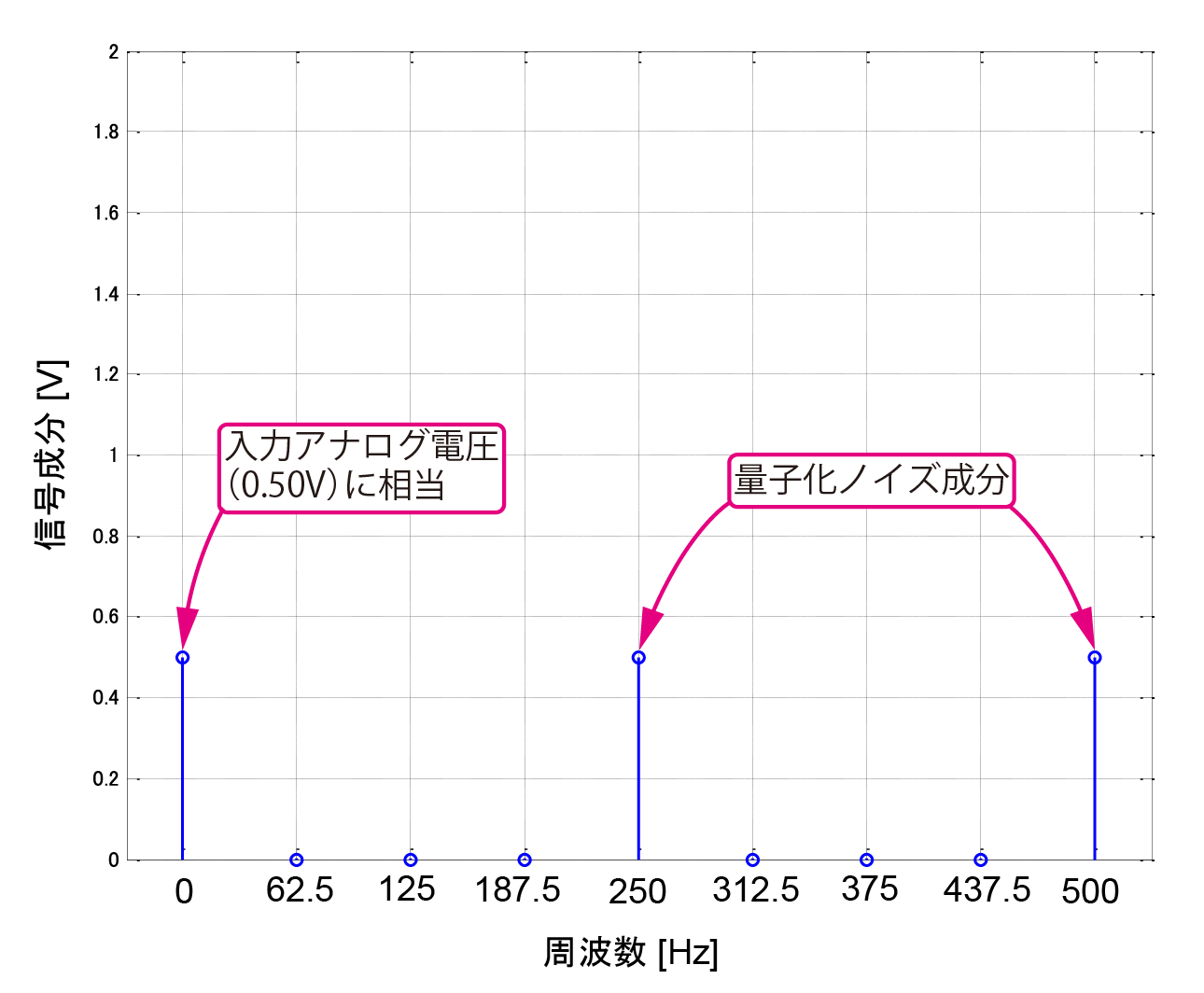
図5に示すのは，図2の16ビット列を，16ポイントFFT（Fast Fourier Transform；高速フーリエ変換）で周波数スペクトルとしたものです．

同じく，図6に示すのは図3の16ビット列を，16ポイントFFTで周波数スペクトルとしたものです．

同じく，図7に示すのは，図4の16ビット列を，16ポイントFFTで周波数スペクトルとしたものです．

入力アナログ電圧は直流であり，同図の直流のところにその電圧成分が得られています．直流以外の周波数のスペクトルは「量子化ノイズ成分」だと考えられます．高い周波数側に量子化ノイズ成分が押しやられているようにも見えます（16ポイントFFTした結果は折り返し部分の9ポイント目，500 Hzまで表示させている）．

繰り返しになりますが，ここまでで得られたことは以下の2点に集約できます．

1. 16ビット列の平均値は入力電圧の大きさになっている
2. 周波数スペクトルで見てみると，量子化ノイズ成分は高い周波数側に押しやられている

4．1次$\Sigma\Delta$変調器のノイズ・シェーピングのしくみを簡単な数式から理解する

ここまで$\Sigma\Delta$型ADCのノイズ・シェーピングのしくみを，どちらかというとイメージ的に示してきました．続いてここでは，このしくみを数式で考えてみましょう．

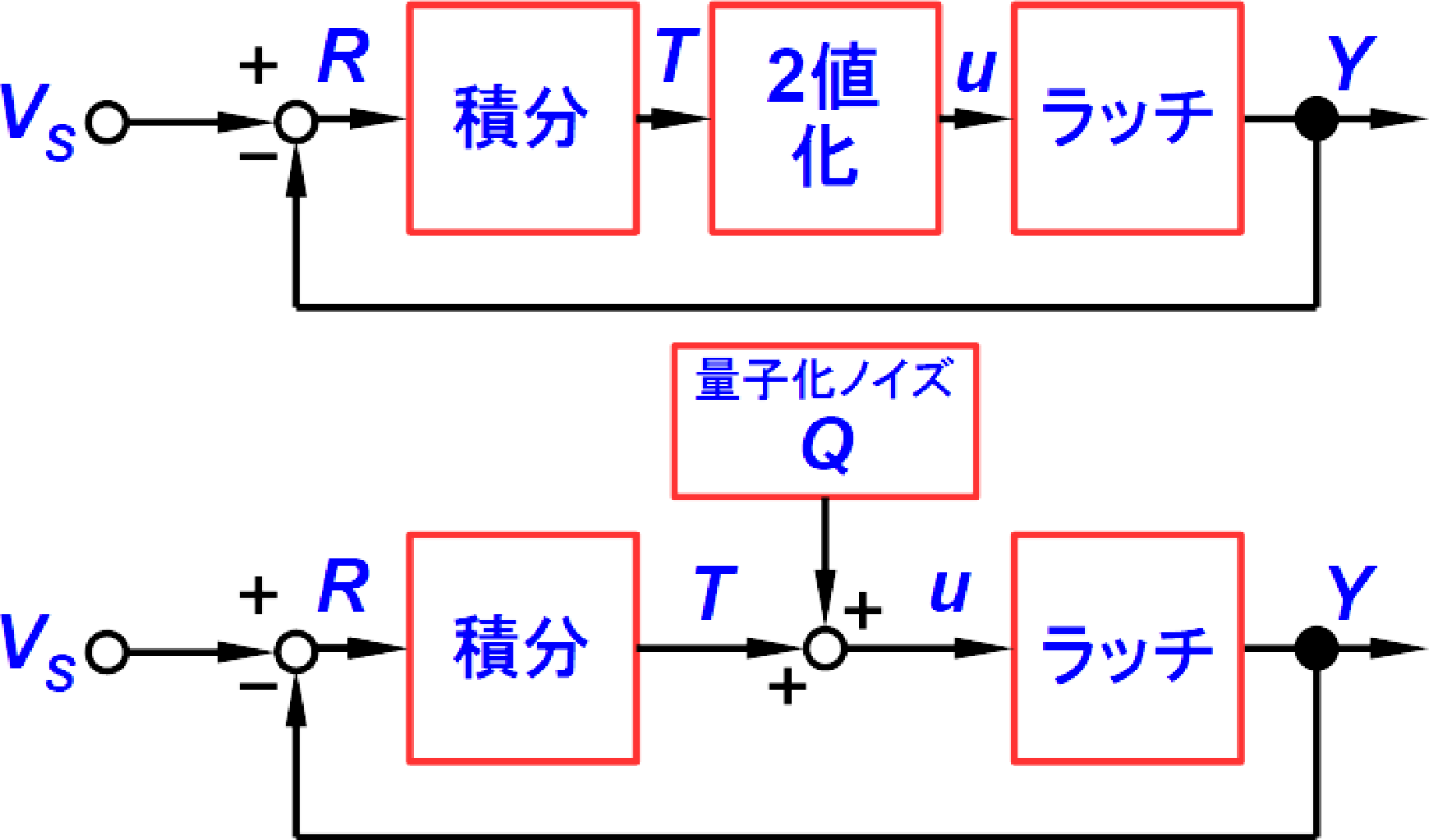
図1の1次$\Sigma\Delta$変調器の部分だけをブロック図として取り出したものが，図8の上の図です．

積分器からの出力電圧$T$が，コンパレータで2値化された（量子化された）電圧$u$になるとき，この差電圧$Q$を「量子化ノイズ$Q$」として考えます．$Q$は式（1）で表します．
\begin{equation} \begin{aligned} Q = u – T \end{aligned} \label{eq:1-1-1} \end{equation}

アナログ電圧$T$が2値化された電圧$u$に変換されるとき，その差分（誤差）$Q$が量子化ノイズになります．

この関係から，ラッチに加わる電圧$u$（2値化された電圧）は，$T$に対して量子化ノイズ$Q$が足しあわされたものとして，同図下のように表すことができます．ラッチ出力$Y$（後段のディジタルLPFに送られるもの）は2値化された電圧であり，ディジタル論理のH/Lの1ビット・データに相当します．

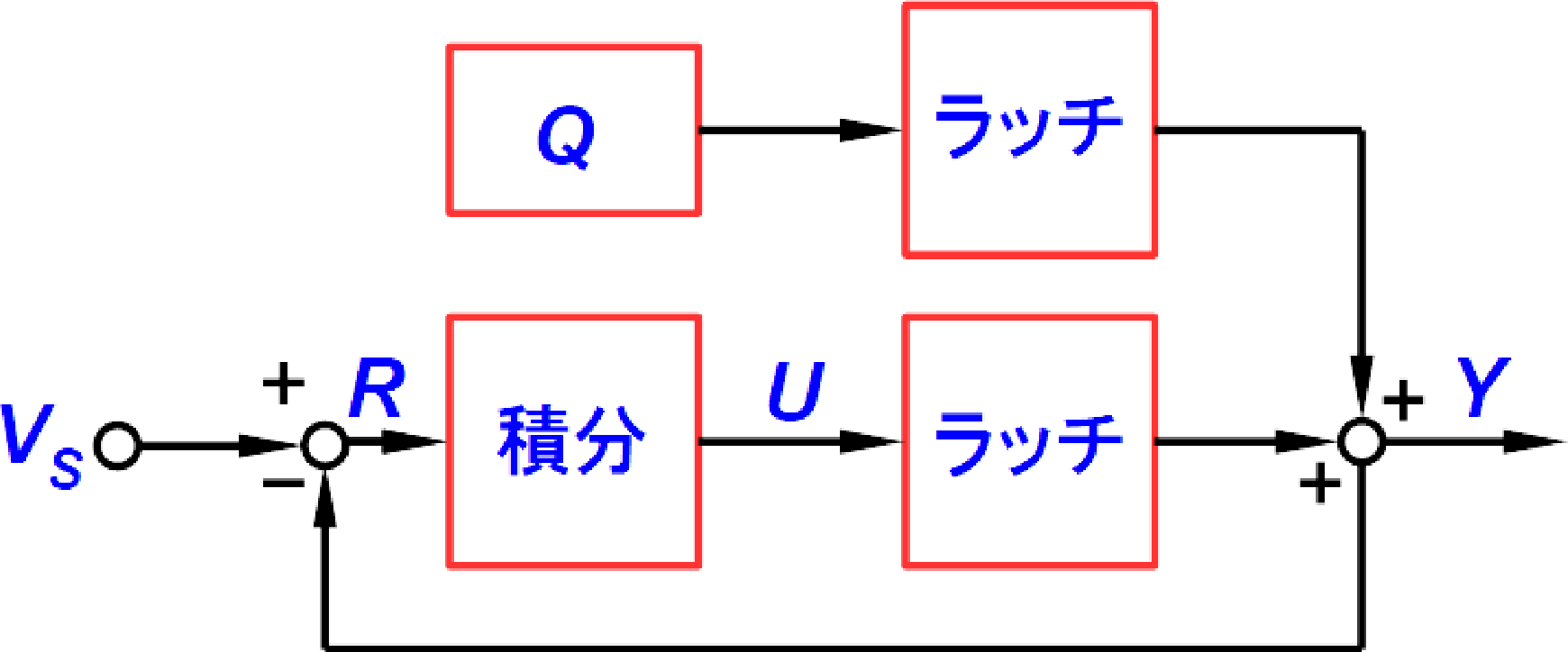
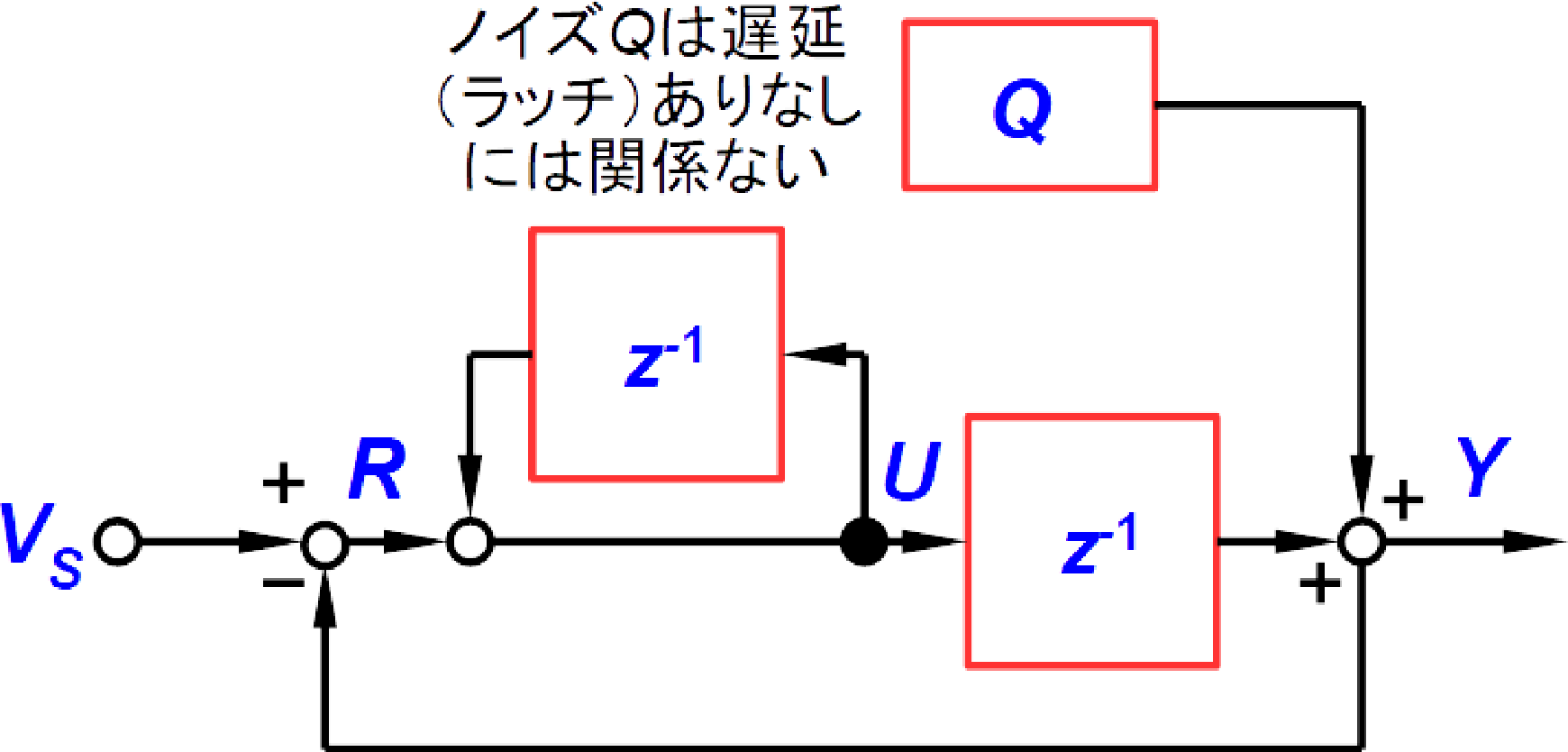
そうするとこの図8の下のブロックは，ブロック線図として考えると，図9のように変形できます．

量子化ノイズ$Q$は単なる誤差量ですから，量子化ノイズ$Q$が足しあわされるようすは，後段にラッチを配置してもしなくても同じです（加わるノイズのタイミングが1サンプルずれるだけ）．そうすれば図9は，図10のように$Q$のラッチを省略できます．

またさらに図10では図9を$z$変換で表しています．「$z$変換」とか$z^{-1}$とかいうと，なんだか難しそうだと思うかもしれませんが，単にディジタルのDフリップ・フロップにより1クロック遅延させるだけのイメージで，その点だけ理解しておけばほぼ十分です．

ここで注目すべき点は，図9でアナログ積分回路だったものが，図10では$z^{-1}$でループ（フィードバック）となるディジタル回路になっていることです．この部分は，図9でアナログ回路として考えれば，$R$を時間積分し$U$として出力する回路に相当し，図10でディジタル回路として考えれば，$R$として入ってきた数値（本来はA-D変換する前のアナログ値だが，ディジタル値になっているとして）を，1サンプル前の時間の数値$U$と足し算し，新しい数値$U$を出力する回路になります．「アナログ」と「ディジタル」という考え方の違いはありますが，図9と図10は「等価」です．

さらに図10のフィードバックとなる部分は式（2）のように変形できます．
\begin{equation} \begin{aligned} U &= R + z^{-1} U \\ U – z^{-1} U &= (1 – z^{-1}) U = R \\ U &= \frac{1}{1 – z^{-1}} R \end{aligned} \label{eq:1-1-2} \end{equation}

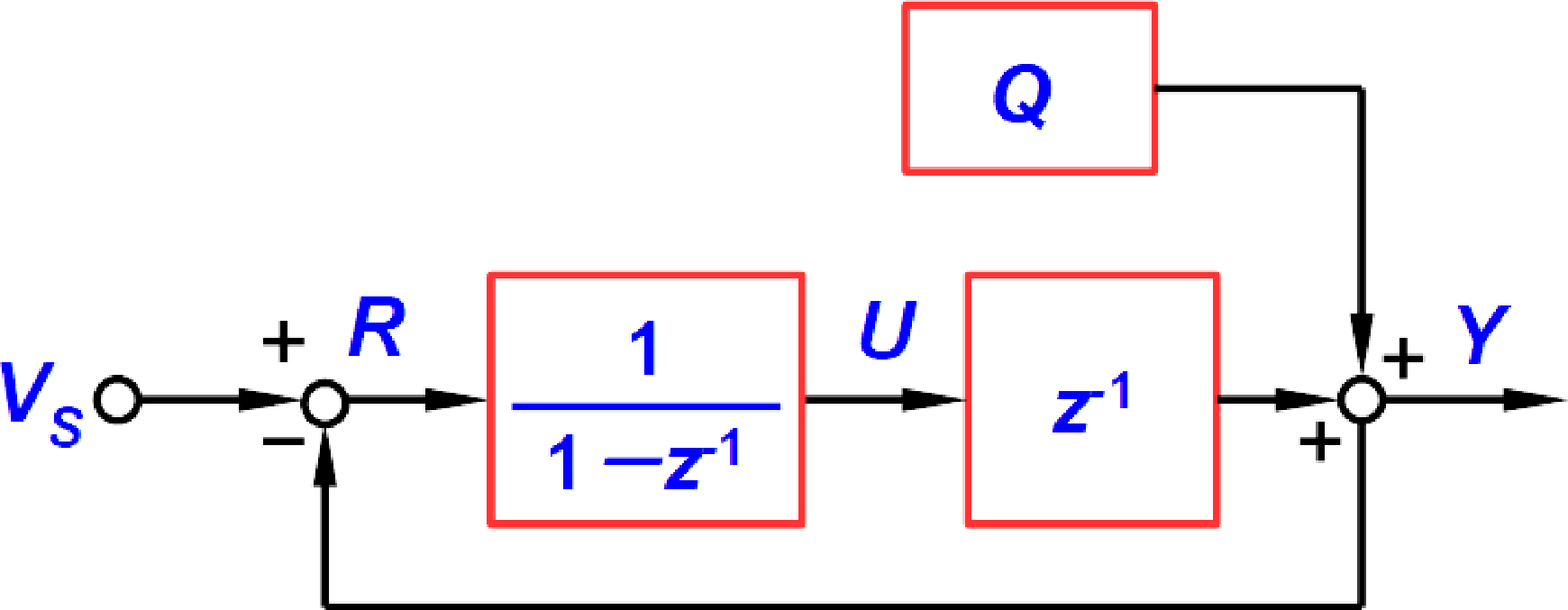
$z^{-1} U$は，1サンプル前の数値に相当します．したがってこれは，図11のように表すことができます．

図11のブロック線図全体を数式で表してみましょう．$V_S$, $R$, $U$, $Y$, $Q$の関係は式（3）で表されます．
\begin{equation} \begin{aligned} R &= V_S – Y \\ U &= \frac{1}{1 – z^{-1}} R \\ Y &= U z^{-1} + Q \end{aligned} \label{eq:1-1-3} \end{equation}

$Y$の式に$U$の式を代入すると，式（4）のようになります．
\begin{equation} \begin{aligned} Y &= \frac{1}{1 – z^{-1}} R z^{-1} + Q \\ Y – Q &= \frac{1}{1 – z^{-1}} R z^{-1} \end{aligned} \label{eq:1-1-4} \end{equation}

ここに$R$の式を代入して整理すると，式（5）のようになります．
\begin{equation} \begin{aligned} Y – Q &= \frac{1}{1 – z^{-1}} (V_S – Y) z^{-1} \\ (Y – Q)(1 – z^{-1}) &= (V_S – Y) z^{-1} \\ (Y – Q) – (Y – Q) z^{-1} &= (V_S – Y) z^{-1} \\ Y – Q – \red{Y z^{-1}} + Q z^{-1} &= V_S z^{-1} – \red{Y z^{-1}} \\ Y – Q + Q z^{-1} &= V_S z^{-1} \\ Y &= V_S z^{-1} + (1 – z^{-1}) Q \end{aligned} \label{eq:1-1-5} \end{equation}

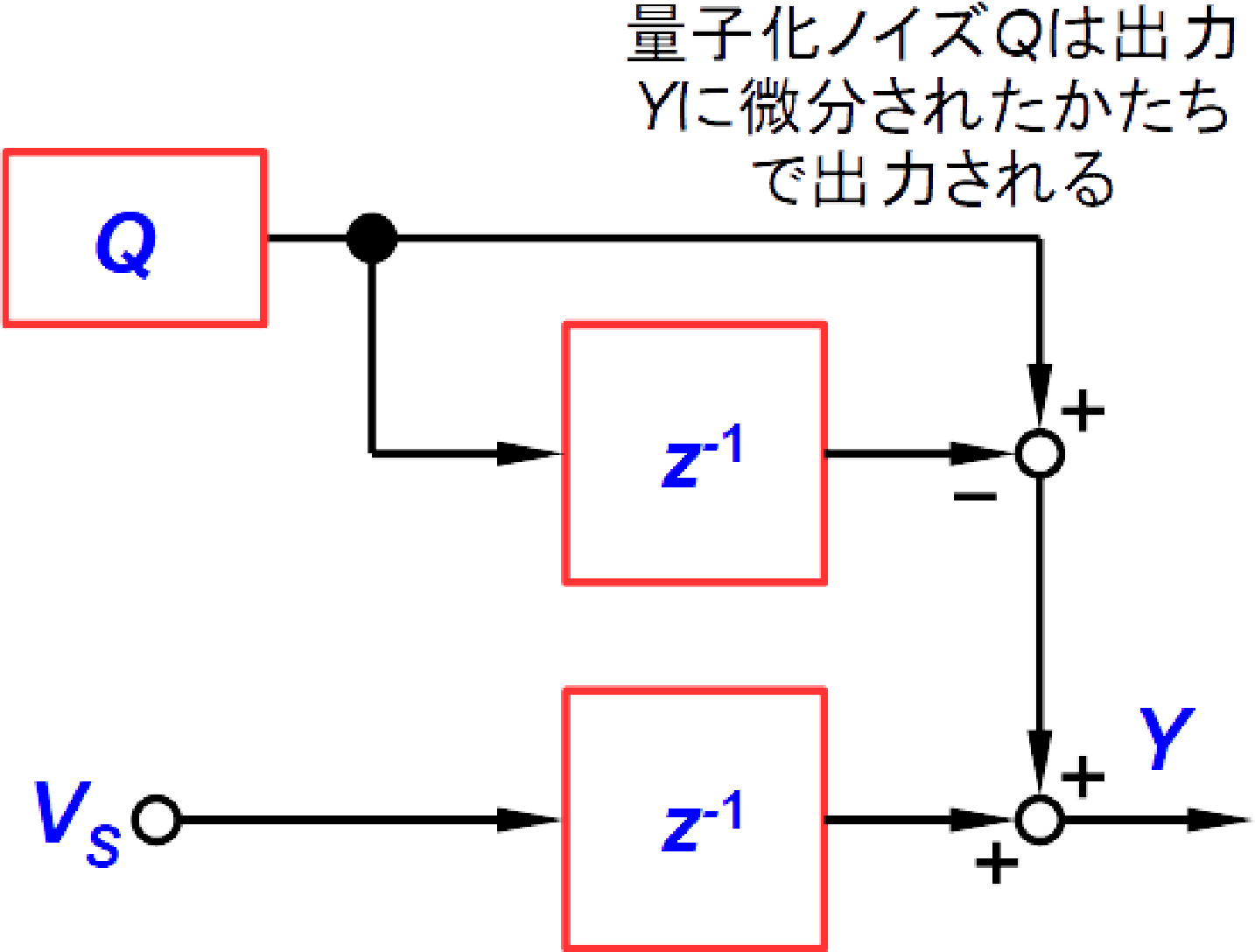
ここで赤の部分は相互に消しあう関係です（式を追いやすいように変形をすべて記載している）．こうするとこの式によるブロック線図は，図12のように表すことができます．

入力電圧$V_S$と出力$Y$との関係（信号伝達関数$H_S$）は式（6）で表されます．
\begin{equation} \begin{aligned} H_S = \frac{Y}{V_S} = z^{-1} \end{aligned} \label{eq:1-1-6} \end{equation}

信号源$V_S$（本来はA-D変換する前のアナログ値だが，ディジタル値になっているとして）が1サンプル遅れて出力$Y$に現れる「素通し」の系になります．

いっぽう量子化ノイズ$Q$と出力$Y$との関係（量子化ノイズ伝達関数$H_Q$）は式（7）で表されます．
\begin{equation} \begin{aligned} H_Q = \frac{Y}{Q} = 1 – z^{-1} \end{aligned} \label{eq:1-1-7} \end{equation}

直接の$Q$とその1サンプル遅れたぶんが引き算されます．これは「微分回路」と考えられ，低い周波数で出力$Y$は$Q$（量子化ノイズ）の大きさが小さくなる，キャンセルされる動作だとわかります．$Q$が固定だと出力$Y$に出てくる値がゼロになることは直観的にも理解できるでしょう．

2次，さらにより高次の$\Sigma\Delta$変調器では，この量子化ノイズ伝達関数$H_Q$の式が，その次数$n$でべき乗となるのですが，話しが難しくなりますし，基本的なうごきとしてはこの1次の場合と同じなので，1次$\Sigma\Delta$変調器のしくみが理解できていれば実用上は十分です．

次回は実際に∑Δ変調器出力のようすを確認してみます．

参考文献

1. アナログ・デバイセズ, 「AD7401 データシート」.
2. アナログ・デバイセズ, 「シグマ・デルタADC/DACの原理」, アプリケーション・ノート AN-283.
3. Walt Kester, The Data Conversion Handbook, Chapter 3: Data Converter Architecture, Analog Devices.
   https://www.analog.com/jp/education/education-library/data-conversion-handbook.html
4. Walt Kester, ADC Architectures III: Sigma-Delta ADC Basics, Tutorial MT-022, Analog Devices.
   https://wcm.cldnet.analog.com/media/en/training-seminars/tutorials/MT-022.pdf
   

---

« ZEPマガジン前の記事「高周波対応シミュレータ Qucsで学ぶアナログ電子回路 超入門［第2回　目指せ50$\Omega$！高周波のインピーダンス］」

ZEPマガジン次の記事「高周波対応シミュレータ Qucsで学ぶアナログ電子回路 超入門［第3回 $L$と$C$でマスタするマイクロストリップ線路］」 »