高周波対応シミュレータ Qucsで学ぶアナログ電子回路超入門

GHz×Gbit時代のハードウェアはパソコンで設計する

反射 1/10！角は切り落とす

著者・講師：市川裕一/Yuichi Ichikawa
企画・編集：ZEPエンジニアリング株式会社

プリント・パターンの曲げと反射

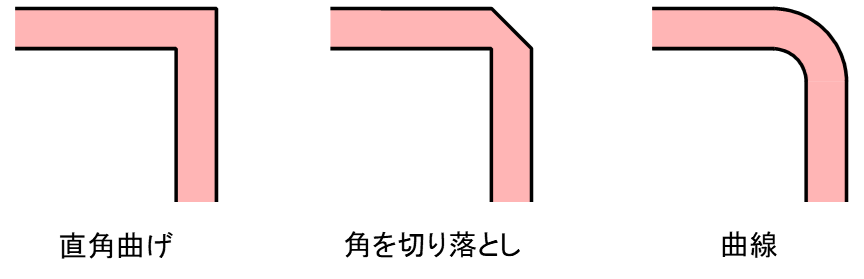
高周波回路や高速ディジタル回路のプリント・パターン設計では，「プリント・パターンを直角に曲げると反射が大きくなるので，曲げの角を切り落とすか曲線で接続する」ということが暗黙の了解です（図1）．


図1　高周波信号にとってプリント・パターン曲げ部は鬼門

急な曲がり角があったら，「角にぶつかって信号がスムーズに進めない」となんとなく想像できます．

なぜ反射が大きくなるのか，今回は「直角の曲げ」を考えてみましょう．

「直角曲げ」vs「角を切り落とした曲げ」

シミュレーションの条件設定

QucsStudioを使って，曲げを1つ設けたプリント・パターンの反射特性を調べます．

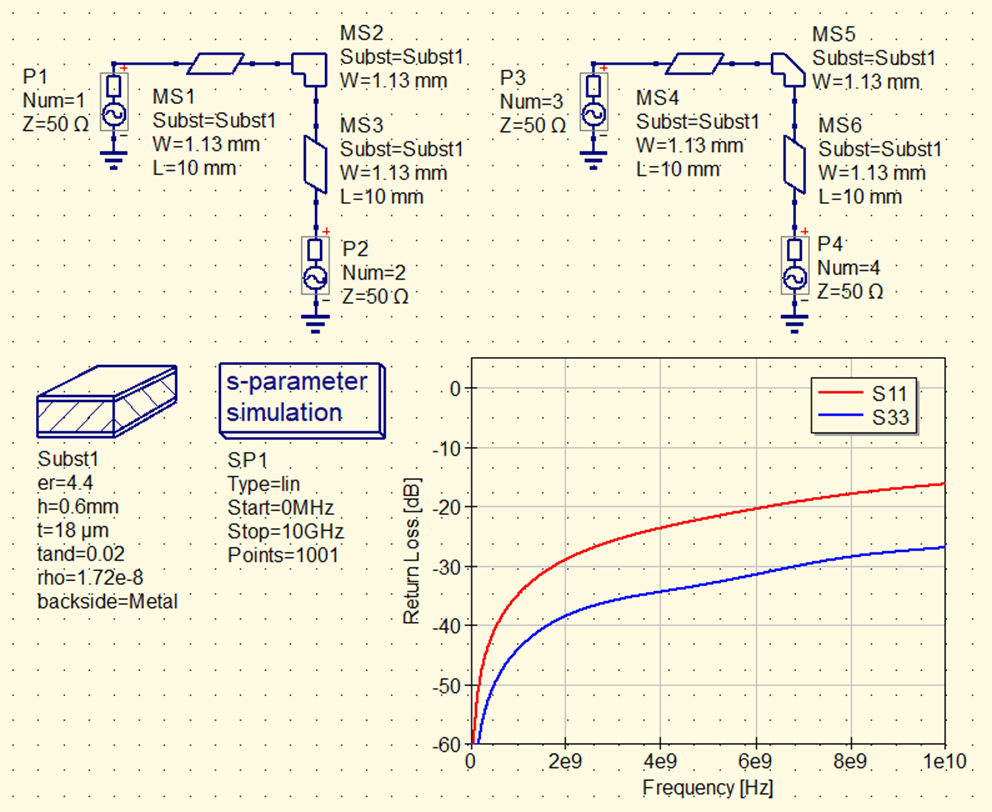
直角に曲げた場合と，角を切り落とした場合で比較してみます．図2にシミュレーション回路とその解析結果を示します．


図2　曲げを1つ設けたプリント・パターンの反射特性比較（直角と角を切り落とし）

ここまで，パターン幅$W=$1mmで話を進めてきましたが，曲げ以外の反射の影響をなくすため，伝送線路計算ツールで特性インピーダンス50$\Omega$のパターン幅を求め，マイクロストリップ線路部品に適用しています．

直角曲げは問題あり

$S_{11}$が直角曲げ（左側回路）の特性，$S_{33}$が角を切り落とし（右側回路）の特性です．

直角に曲げた場合の特性が，思っていたよりも悪くないと感じた方も多いのではないでしょうか．

シミュレーション結果では，6GHz以下ではリターン・ロスが20dBを超えています（反射係数は1/100以下）．

数GHz以下では直角の曲げをそのまま残しても問題がなさそうですが，曲げが複数個所あるとその影響が積み重なってくるので対策すべきです．

角を切り落とすと反射は1/10に

2つの曲げの特性を比較してみると，全帯域でリターン・ロスが約10dB違います．つまり角を切り落とすことで，反射が1/10に減少します．

直角曲げと角を切り落とした曲げの特性インピーダンス

直角の曲げの何が反射特性を悪くしているのか調べてみましょう．

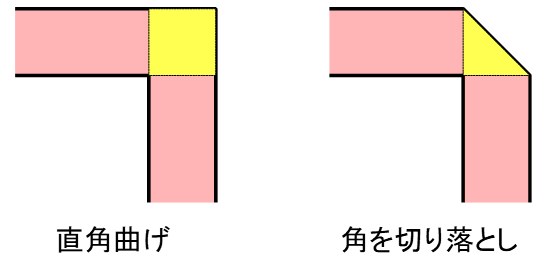
図3に曲げの部分の拡大図を示します．


図3　直角のほうが角切り落としより曲げ部の面積が大きい

色を変えた部分のプリント・パターンを比較して，何か気づきませんか？曲げの部分のプリント・パターンの面積が違います．曲げの部分の面積を比較すると，直角に曲げた場合は，角を切り落とした場合の2倍です．

式\eqref{eq:2_l_patten}と式\eqref{eq:3_capacitance}はプリント・パターンのインダクタンスとキャパシタンスを求める式です．

\begin{align} L_P = 0.2 \times L \left[ \ln \left( \dfrac{2L}{W+t} \right) + 0.2235 \times \left( \dfrac{W+t}{L} \right) + 0.5 \right] \, [\text{nH}] \label{eq:2_l_patten} \end{align} \begin{align} C_P=\varepsilon_r \varepsilon_0 S/d \label{eq:3_capacitance} \end{align}

式\eqref{eq:2_l_patten}から，直角の曲げでは角が出っ張り，プリント・パターン幅$W$が広くなっているので，インダクタンスは小さくなります．

式\eqref{eq:3_capacitance}から，直角の曲げではプリント・パターンの面積$S$が大きくなっているので，キャパシタンスが大きくなります．

つまり，特性インピーダンスを求める式\eqref{eq:5_characteristic_impedance}において，$L$が小さくなり，$C$が大きくなるので，特性インピーダンスが小さくなります．

\begin{align} Z_0=\sqrt{\dfrac{j \omega L}{j \omega C}}=\sqrt{\dfrac{L}{C}} \label{eq:5_characteristic_impedance} \end{align}

その結果，直角曲げとその前後の直線部分では特性インピーダンスが違うため，反射が起こります．角を切り落とすと，インダクタンスの減少とキャパシタンスの増加を抑えられて，特性インピーダンスの変化が抑えられます．

高周波信号は特性インピーダンスが変化しない伝送路を好む

曲げに限らず，プリント・パターンの形状や寸法が変化する部分では，プリント・パターンの特性インピーダンスが変化し，反射を起こす可能性があります．

プリント・パターンを水（信号）が伝わる水路と考えると，曲げをはじめとする「変化」の影響をイメージしやすいと思います．

周波数の低い信号は波長（周期）が長いので，水路の水面がゆっくり上下して伝わります．その途中で水路の形状に多少の変化があっても，その上下動はほとんど影響を受けることなく伝わって行きます．周波数の高い信号の波長（周期）は短いので，水路の形状に変化があると，その影響を受けて波に変化が起こります．

プリント・パターンを設計する際は，信号の波長を意識し，プリント・パターンを伝わって行く信号の波をイメージすることが大切です．高周波信号は急激な特性の変化が嫌いです．どうしても変化が避けられない部分は，できるだけ緩やかに変化するようなアートワークを心がけてください．

コラム　波長はプリント・パターン上で短くなる

自由空間と伝送線路上の波長は違う

自由空間における1GHz信号の波長$\lambda_0$は，式\eqref{eq:6_lambda_zero}で求められます．

\begin{align} λ_0=\dfrac{c}{f}=\dfrac{3 \times 10^8\text{m/s}}{1\times 10^9\text{Hz}}=0.3 \text{m}=30 \text{cm} \label{eq:6_lambda_zero} \end{align}

ただし，$c$は光速（3$\times$10$^8$m/s），$f$は周波数［Hz] です．

信号の波長は，伝送線路上でも自由空間と同じなのでしょうか？QucsStudioで，マイクロストリップ・ラインを通過特性を確認し，その位相変化から，信号の波長を求めてみましょう．

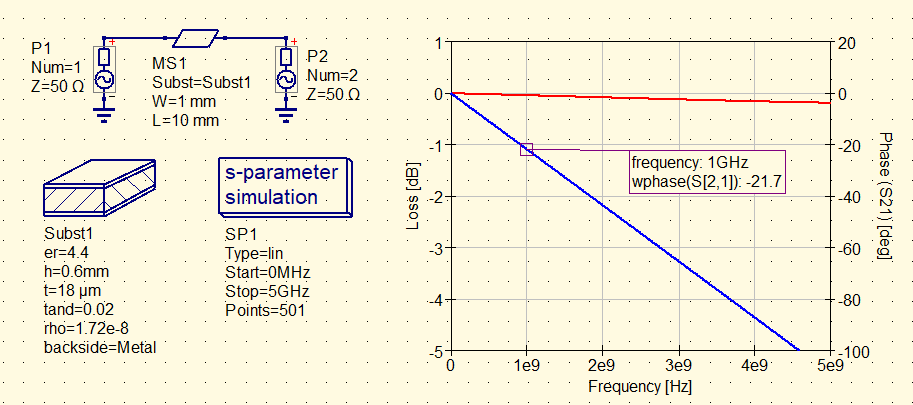
図4にシミュレーション回路とその通過位相特性を示します．


図4　位相変化の解析はQucsの伝送線路計算ツールが便利

図4にマーカで示した1GHzでの信号の波長$\lambda_g$を求めてみましょう．プリント・パターンの長さが1cm（10mm）なので，式\eqref{eq:6_lambda_zero}と式\eqref{eq:7_lambda_g}から，16.59cmと求まります．

\begin{align} λ_g=\dfrac{360^\circ}{\theta \times L}=\dfrac{360^\circ}{21.7^\circ} \times 1\text{cm} = 16.59\text{cm} \label{eq:7_lambda_g} \end{align}

ただし，$\theta$は位相変化，$L$はプリント・パターンの長さです．

プリント・パターン上では波長が縮む

自由空間での波長$\lambda_0$に対する，伝送線路上での波長$\lambda_g$の比率を「波長短縮率」と呼びます．

波長短縮率$k$は，式\eqref{eq:12_wavelength_shortenrate}で求められます．

\begin{align} k=\dfrac{\lambda_g}{\lambda_0} \label{eq:12_wavelength_shortenrate} \end{align}

マイクロストリップ線路上での波長短縮率$k$を式\eqref{eq:12_wavelength_shortenrate}で求めてみると，次のとおり，式\eqref{eq:6_lambda_zero}，式\eqref{eq:7_lambda_g}，式\eqref{eq:12_wavelength_shortenrate}から0.553です．

\begin{align} k=\dfrac{16.59 \text{cm}}{30\text{cm}}=0.553 \label{eq:13_shortenrate_k} \end{align}

つまり，厚さ0.6mmのFR-4基板上のマイクロストリップ線路（特性インピーダンスはほぼ50$\Omega$）において，信号の波長は自由空間の約55$\%$（約1/2）になります．

伝送線路計算ツールを使うと位相変化が簡単に求まる

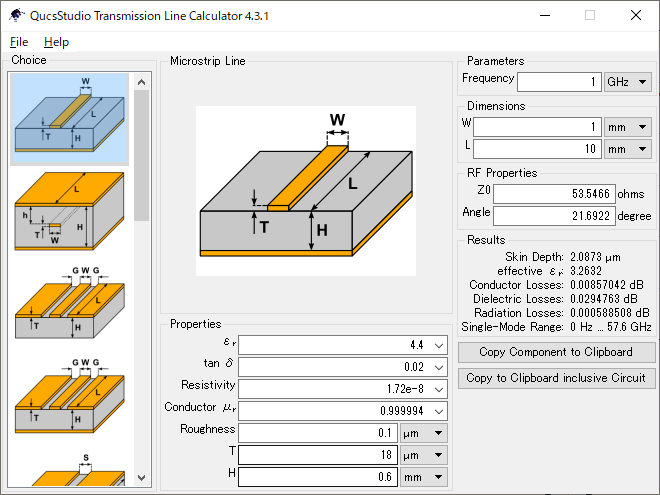
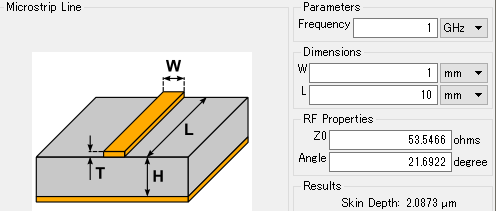
図4の位相変化は，図5の伝送線路計算ツールを使うと簡単に求められます．


図5　位相変化の解析はQucsの伝送線路計算ツールが便利

$Z_0$の結果表示の下に位相変化量が表示されています（図6）．この位相変化量のことを，電気長（electrical length）といいます．


図6　伝送線路計算ツールでの位相表示

プリント・パターンの長さが10mmのとき「1GHzでの電気長は$21.69^\circ$」と言います．同じパターンでも，周波数が変われば信号の波長も変わるので，電気長も変わります．

周波数が2倍になれば波長は1/2になるので，電気長は2倍になります．電気長で表す場合は，どの周波数における電気長なのか明示しましょう．

電気長は位相のほかに波長でも表されます．電気長 $90^\circ$ は「1/4波長」または“（1/4）$\lambda$”と表されます．ちなみに，図5のツールの「Angle」に「360」と入力すると，プリント・パターン長$Ｌ$には伝送線路上での波長$\lambda_g$が表示されます．

高周波対応シミュレータ Qucsで学ぶアナログ電子回路 超入門