高周波対応シミュレータ Qucsで学ぶアナログ電子回路 超入門

GHz×Gbit時代のハードウェアはパソコンで設計する

$L$と$C$でマスタするマイクロストリップ線路

• 著者・講師：市川 裕一/Yuichi Ichikawa
• 企画・編集：ZEPエンジニアリング株式会社

「マイクロストリップ線路」は，高速ディジタル信号や高周波アナログ信号を伝送するプリント基板設計に利用される定番の伝送線路です．本稿では，$S$パラメータ解析が可能なフリーの電子回路シミュレータ QucsStudioを動かしながら，信号伝送に使われるマイクロストリップ線路（伝送線路，プリントパターン）が一体何なのか見て行きます．

プリント・パターンのもつ$L$と$C$を計算してみよう

長さ10mmの例題線路

本連載第1回で，図1に示すマイクロストリップ線路の各寸法を$W$=1mm，$t=18\mu$m，$L$=10mm，$h$=0.6mm，FR-4基板，$\varepsilon=$4.4としたときの，プリント・パターンがもつインダクタンス$L_P$とキャパシタンス$C_P$を求めました．

インダクタンスは7nH

図1に示すプリント・パターンのインダクタンス$L_P$は，式\eqref{eq:2_l_patten}から7nHです．

\begin{align} L_P = 0.2 \times L \left[ \ln \left( \dfrac{2L}{W+t} \right) + 0.2235 \times \left( \dfrac{W+t}{L} \right) + 0.5 \right] \, [\text{nH}] \label{eq:2_l_patten} \end{align}

平行平板と仮定すると0.65pF

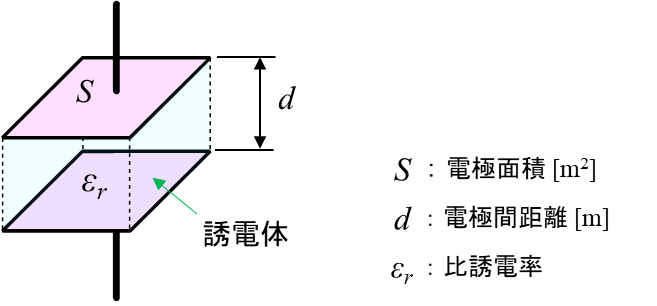
図1に示すマイクロストリップ線路が，図2に に示す平行平板構造だと仮定すると，そのキャパシタンスは，式\eqref{eq:3_capacitance}から0.65pF と計算できます．

\begin{align} C_P=\varepsilon_r \varepsilon_0 S/d \label{eq:3_capacitance} \end{align}

ただし，$\varepsilon_0$は真空の誘電率（$8.854 \times 10^{-12}$）［F/m］です．

特性インピーダンスを計算してみる

QucsStudioの伝送線路計算ツールで計算

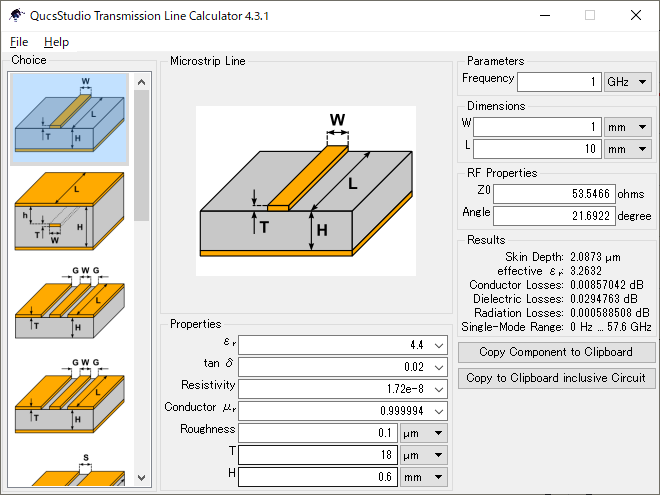
QucsStudioの伝送線路計算ツールで，マイクロストリップ線路（図1）の特性インピーダンス$Z_0$を求めると53.55$\Omega$（約50$\Omega$）です（図3）．

特性インピーダンスの式で計算

特性インピーダンスを求める式\eqref{eq:characteristic_impedance2}に先ほど求めた$L_P$と$C_P$を代入すると103.8$\Omega$です．

\begin{align} Z_0=\sqrt{\dfrac{j \omega L}{j \omega C}} = \sqrt{\dfrac{L}{C}} \label{eq:characteristic_impedance2} \end{align}

2つの計算結果の違いはなに？

図2の平行平板キャパシタは，向かい合う2つの電極の面積が等しくなっています．

一方，図1のマイクロストリップ線路では信号線に対向するベタ・グラウンドの面積が非常に大きくなっています（理想的には無限大）．したがって，キャパシタンスは0.65pFより大きくなるはずです．

式\eqref{eq:characteristic_impedance2}から，$L_P$=7nHとして，特性インピーダンス$Z_0$が53.55$\Omega$になる，キャパシタンス$C_{P\alpha}$を求めると2.44pFです．

$L$と$C$のペアだからこそ高周波伝送できる！

QucsStudioでプリント・パターンがもつ$L$と$C$の影響を確認

連載第1回目と同様に，プリント・パターンの等価素子として，インダクタンス$L_P$だけが存在したとき，そしてキャパシタンス $C_{P\alpha}$だけが存在したときの通過特性を調べます．

$L_P$だけの通過特性

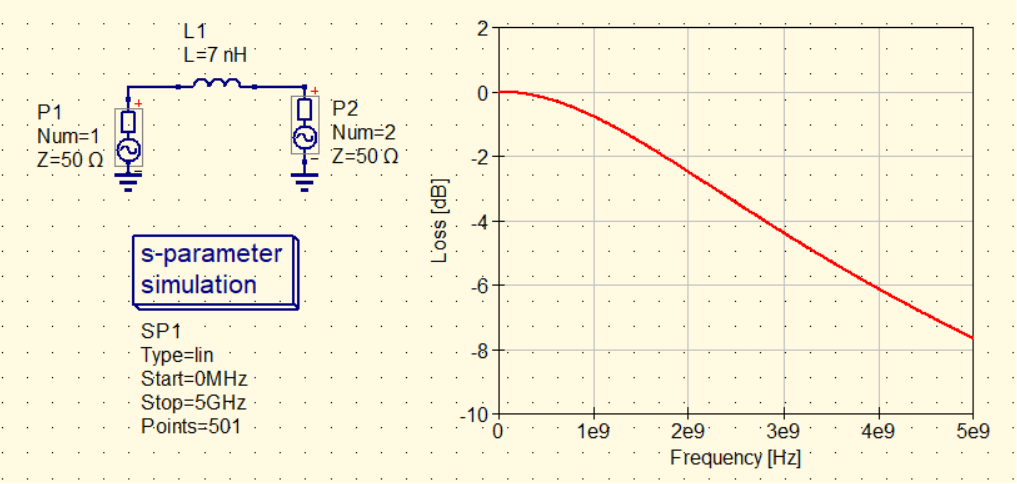
図4は，インダクタンス$L_P$だけのときの通過特性です．周波数が高くなるにしたがって信号が減衰します．

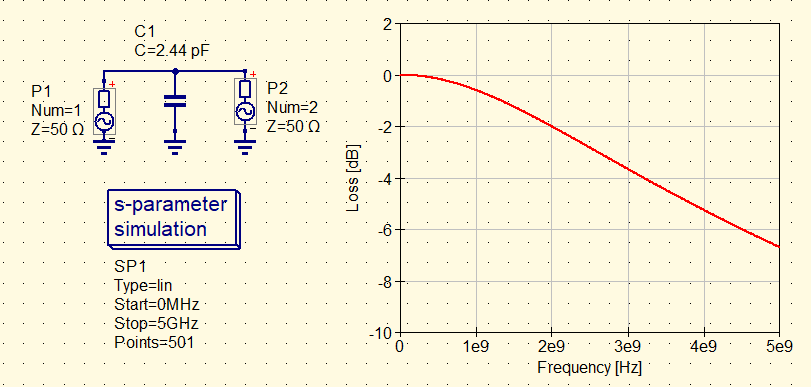
$C_{P\alpha}$だけの通過特性

図5に示すのは，キャパシタンス $C_{P\alpha}$だけのときの通過特性です．図4と同様に，周波数が高くなるにしたがって信号が減衰します．

$L$と$C$が組み合わさると通過特性が平坦になる

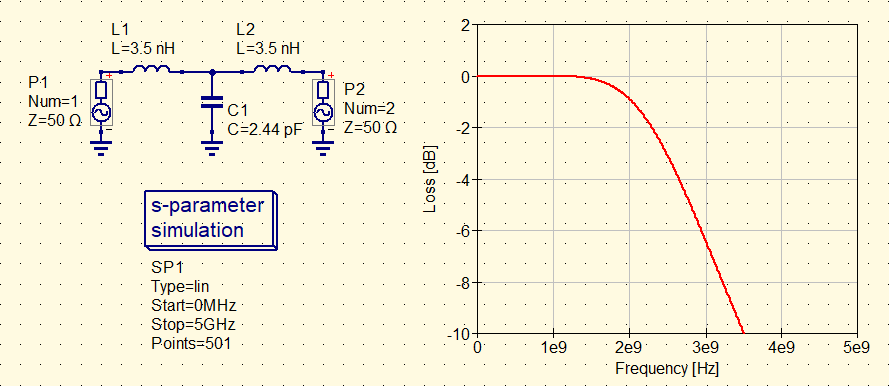
図6に示すのは，$L$=10mmのマイクロストリップ線路の等価回路と通過特性です．

等価回路は，先に求めたインダクタ$L_P$とキャパシタ$C_{P\alpha}$で構成されていますが，元の伝送線路が入出力対称なので，回路も対称になるようインダクタンス$L_P$を2つに分割して配置しました．

2GHz以上での減衰特性が急峻なLPFになっていますが，1.5GHz以下では，通過特性は平坦で信号の減衰がほとんどありません．ここがポイントです．

もっと高い周波数まで信号を通せないのか？

信号を通せるのが1.5GHzではあまりにも低すぎます．

図6の結果は，例題として長さ$L=$10mmのマイクロストリップ線路を，集中定数回路の$L_P$と$C_{P\alpha}$に置き換え，長さの影響を無視しています．

そこで，長さを短くしたときの通過帯域の変化を調べます．

長さを5mmにしたら

$L=$5mmとして，式\eqref{eq:2_l_patten}でインダクタンス$L_P$を求めると2.83nHになりす．

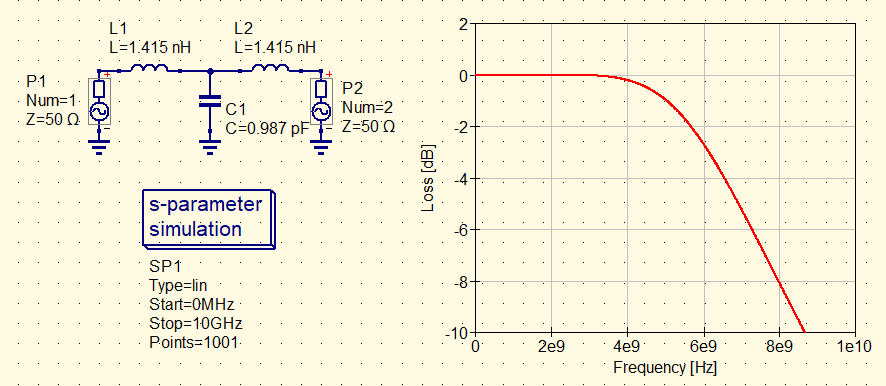
この値を式\eqref{eq:characteristic_impedance2}に代入してキャパシタンス$C_{P\alpha}$を求めると0.987pFです（$Z_0=53.55\Omega$）．

図7に示すのは，長さ5mmのマイクロストリップ線路の等価回路と通過特性です．

カットオフ周波数は約6.2GHzで，図6の10mmの場合よりも2倍以上高くなっています．先ほどと同様に，インダクタンス$L_P$を2つに分割して配置しています．

長さ5mmを2つつないで10mmにしたら

図8に示すのは，図7の回路を2つ直列に接続した長さ10mmのマイクロストリップ線路の等価回路と通過特性です．

カットオフ周波数は約5.5GHzです．5mmの通過特性より少し劣化しますが，図6の2倍以上です．

もっと短くしたら通過特性はどうなる？

プリント・パターンをさらに短くして行けば，カットオフ周波数はいくらでも高くなると予想されます．

しかし短くしすぎると，長さが幅より短くなり，幅と長さが入れ替わり，幅が長手方向になってしまいます．つまり，この考えた方が通用するのは「長さ＞幅」の範囲に限られます．

長さが幅に近づいてくると，インダクタンス$L_P$を求める近似式\eqref{eq:2_l_patten}の精度が落ちてきます．長さは少なくとも幅の2～3倍以上と考えるべきです．

もっと短い長さで解析を試したい場合はどうしたらよいのでしょうか？一番簡単なのは幅を細くすることです．基板の厚さ$h$を薄くすれば，特性インピーダンスを保ったまま，幅を細くすることができます．

マイクロストリップ線路を例に説明してきましたが，ストリップ線路（Strip Line）やコプレーナ・ウェーブガイド（Coplanar Waveguide）など他の伝送線路でも基本は同じです．

コラム　2.5mmのマイクロストリップ線路の通過特性

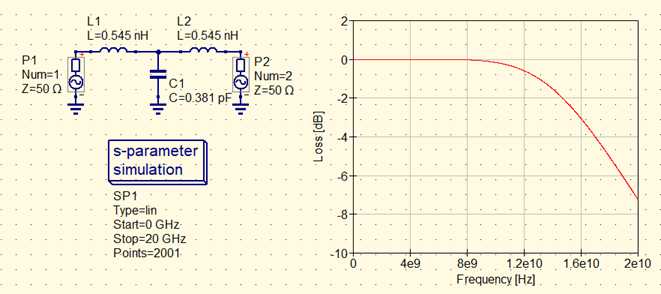
図9に示すのは，長さが2.5mmのマイクロストリップ線路の通過特性です．$L_P$を2つに分割して配置してシミュレーションしました．

インダクタンス$L_P$は，式\eqref{eq:2_l_patten}から1.091nHです．この値を式\eqref{eq:characteristic_impedance2}に代入してキャパシタンス$C_{P\alpha}$を求めると0.381pFです．

カットオフ周波数は約16GHzで，長さ10mmの線路（図6）の約6.4倍，長さ5mmの線路（図7）の約2.6倍です．

$L_P$の計算精度が落ちますが，さらに短くしたり，基板を薄くしてみたりして，通過特性や特性インピーダンスの変化をシミュレーション実験してください．

参考文献

1. 市川 裕一（I-laboratory），高周波回路の設計と製作，誠文堂新光社．
2. 市川 裕一（I-laboratory），はじめての高周波測定，CQ出版株式会社．
3. 市川 裕一（I-laboratory），復刻版 GHz時代の高周波回路設計【オンデマンド版】，CQ出版株式会社．
4. 加藤 隆志（株式会社ラジアン），5G時代の先進ミリ波ディジタル無線実験室，ZEPエンジニアリング株式会社．
5. 知念 幸勇，［VOD/KIT］3GHzネットアナ付き！RF回路シミュレーション＆設計・測定入門，ZEPエンジニアリング株式会社．
6. 川口 正，［VOD/KIT］ポケット・スペアナで手軽に！基板と回路のEMCノイズ対策 10の定石，ZEPエンジニアリング株式会社．
7. 池田 浩昭， ［Webinar/Book/data］電磁界シミュレーションによるプリント基板設計\&EMC対策， ZEPエンジニアリング株式会社．