5V入力/3～28V可変の3W実験用フライバック電源設計

感電防止/手差し部品/USB対応！トランスの作り方をStep by Step解説

• 著者・講師：並木 精司 / Seiji Namiki
• 企画・編集：ZEPエンジニアリング株式会社

インデックス

1. スイッチング電源の回路方式
2. フライバック・コンバータの回路設計
3. トランス設計その1：1次側のインダクタンスと鉄心の選定
4. トランス設計その2：線材と巻き数の計算
5. 入出力回路と制御回路の設計
6. 性能と考察

第1回　スイッチング電源の回路方式

メーカ製にない手軽さとフィールド利用を実現

電子回路の開発は，試作と実験の繰り返しです．無線を利用することの多い現代では，屋外利用装置の開発案件も増えています．

通常，試作回路を実験的に動かすときは，メーカ製の出力電圧可変機能や保護機能を備えた電源測定器を入手します（A＆D製AD-8723Dなど）．しかし，可変出力の本格的な実験用電源は安くありませんし，屋内利用が前提の100V入力仕様です．

試作回路の電源が5V単一ならば，USBバス・パワーを利用できますが，今どきのほとんどの電子回路は，12Vや3.3Vなど複数の電源電圧を必要とします．一見，12V固定出力のACアダプタを使うのが手軽そうですが，いつか実験室はACアダプタだらけになるでしょう．

そこで，USB対応の出力電圧・出力電流可変のデスクトップ電源を自作しました．広範囲に電圧設定と定電流設定ができるコンパクトな可変電源です．図1に外観を示します．

スイッチング電源の設計の学習にもぴったりです．AC100V入力の電源は設計が高度で，初学者には不向きです．本稿で紹介する5Vの低い入力電圧で動く電源なら設計も簡単で，壊れにくく，感電の恐れもありません．

ディジタル回路がどんなに発展してもそれを支えるのはアナログ技術です．派手な所はないですが重要な技術ですので多くの若いエンジニアの人達にぜひ習得して頂けることを期待しています．

目標仕様

電子工作や実験・研究には十分！USB対応

USBバス・パワー対応とします．モバイル・バッテリが使えるので，フィールドでの実験も可能です．

規格では，USB2.0の1ポートからは500mA，USB3.0の1ポートからは900mA取り出すことができます．USB2.0の場合，入力電力は2.5W（=5V$\times$0.5A）ですから，DC-DCコンバータの効率を70$\%$と仮定すると，得られるパワーは1.75W（5V/350mA）です．小信号アナログ回路やマイコン応用回路開発，電子工作には十分です．

出力電圧可変

ディジタル回路の電源電圧は3.3Vまたは5Vです．また，OPアンプが使われることの多いアナログ回路の多くは，12Vまたは15Vが一般的です．一部工業制御系では24Vが使われます．

そこで，出力可変範囲は，ロジック用の3.3Vから制御回路用24Vまでカバーします．

電圧設定は，多回転精密可変抵抗器で大まかな設定を行い，さらにもう一つの可変抵抗器により微調整できるようにします．

安全電圧42.4V以下に収める

回路電圧も安全規格で定める安全電圧「42.4V以下」に収めます．回路に手で触れても感電の危険がありません．

12V出力時最大3W

スマホ充電用のUSB対応ACアダプタが市販されています．出力定格は5V固定/最大1Aが一般的です．

ACアダプタのUSB出力ポートから電源を供給すると，12V出力時，最大約3Wまで出力を取り出すことができます．

出力電流リミッタ付き

試作回路が短絡していたときに，電源回路が壊れてしまわないように，定電流出力機能を搭載します．定電流値は多回転可変抵抗で0～0.3Aで任意に設定できます．

出力電圧が高い時は，電源制御IC LT1172CN8（アナログ・デバイセズ製）が備える過電流制限機能が働くため出力電力が制限され，0.3Aを出力できないことがあります．

LEDの定電流駆動やニッケル水素蓄電池やリチウム・イオン蓄電池の充電にも使用できます．

入出力コネクタ

入力コネクタはUSB Mini-Bを採用しました．出力コネクタは使い勝手を考慮してワンタッチ端子台を選択します．

プリント基板の寸法

基板の寸法は，美観と信頼性を考慮してオプションで，ポリカーボネート・ケースP-00358（秋月電子通商，透明，95$\times$65$\times$23mm）に収納できる大きさとしました．ただし，ケースの入力部，可変抵抗器，出力ワンタッチ端子台部分は自分で穴加工が必要です．

はんだ付けが簡単な手挿し部品対応

初めて電子回路を製作する方でも，比較的簡単に自作できるように，すべてリード付きの手挿し部品を選び，片面実装としました．電源容量の割に基板が大きめですが，実装の簡単さを優先しました．

応用

1セル・リチウム・ポリマ蓄電池の充電

本電源の定電圧定電流特性を利用して，リチウム・ポリマ蓄電池を充電できます．通常，リチウム・ポリマ蓄電池は，CVCC（定電圧定電流）充電方式で充電します．

CVCC充電方式は，電池電圧が低い期間は定電流で充電を行い，充電終止電圧に近づいたら定電圧充電に切り替える方式です．

本電源を使って充電するときは，無負荷時の出力電圧をリチウム・ポリマ蓄電池の充電終止電圧である4.2V±50mVに設定します．定電流値は，電池の定格放電電流と同じ電流に調整します．定格放電電流で充電することを「$1C$充電」と言います．

電池メーカは$1C$充電を勧めていますが，少し劣化の進行が速くなります．$2C$程度なら問題ないようです．

充電終止電圧は正確に設定する必要があります．充電終止電圧設定が高いと，過充電になって電池にダメージを与えます．最悪発熱発火します．逆に設定電圧が低すぎると満充電になりません．

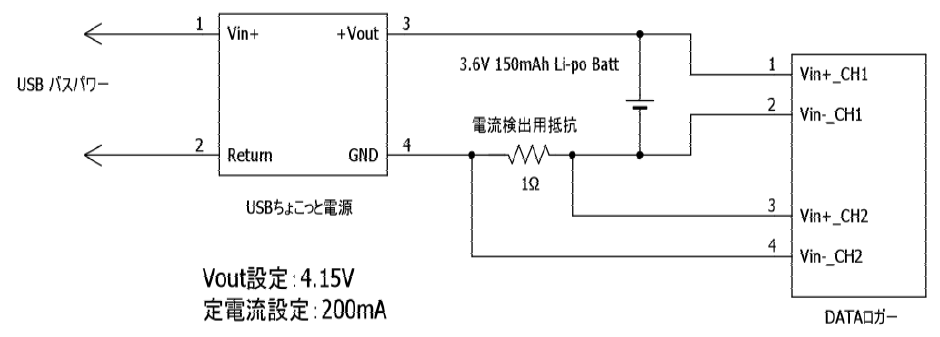
実際，3.6V/150mAhの1セルのラジコン用リチウム・ポリマ蓄電池を使って実験しました．無負荷時の出力電圧は4.15Vに設定，充電電流は$1.33C$の200mAに設定しました．電流はダミー抵抗を接続してあらかじめ設定しました．

今回の電池では3.6V時に200mAになるように設定するので，ダミー抵抗は18$\Omega$（=3.6V/0.2A）になります．

まず無負荷で出力電圧を正確に4.15Vに設定し，出力端子に18$\Omega$の抵抗を接続して，出力電圧が3.6Vになるように，電流設定可変抵抗を調整すれば定電流設定は200mAです．電流計を使って，直接電流値を測定してもOKです．

ただし，充電時には電流計をショートしてください．意外にも電流計の内部抵抗は無視できないほど大きく，充電特性に大きく影響を与えます．

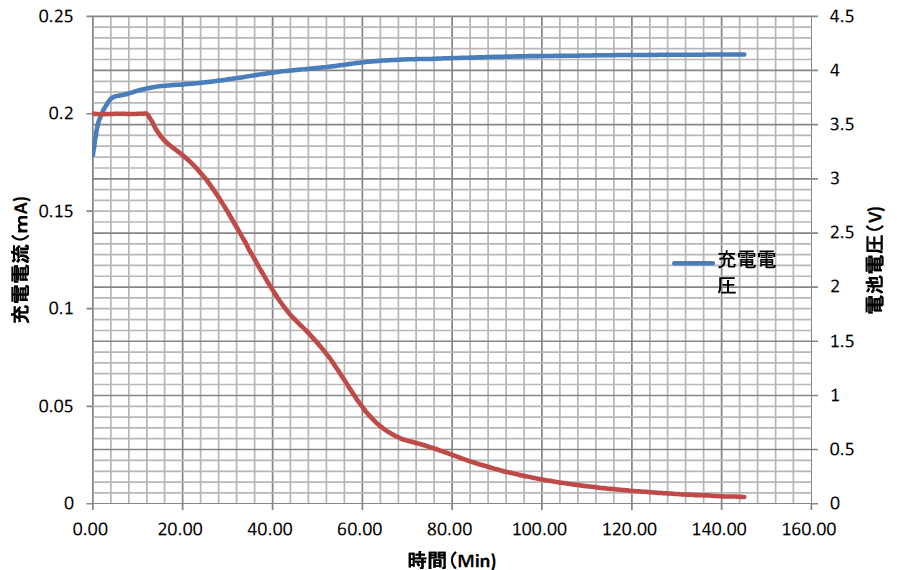
図2に充電特性を示します．

図3にその測定回路を示します．

電圧，電流の変化はデータ・ロガーGL220（グラフテック社製）を使って記録しました．電流は1$\Omega$の両端電圧を測定しています．

リチウム・ポリマ蓄電池を2.8Vまで放電してから充電を開始しました．最初の12分の充電電流は200mAです．その後は電池電圧が高くなるにつれ充電電流が徐々に減ります．今回，1$\Omega$を直列に入れて電流を測定した影響で，約3.9Vから電流が減少しています．この抵抗がなければ4.1Vまで200mAの定電流充電ができて，もっと短時間で満充電になります．

電池電圧が設定電圧の4.15Vに接近すると，充電電流は非常に小さくなります．電池電圧が充電終止電圧になったら満充電です．

多セルのリチウム・ポリマ蓄電池は充電バランス回路が必要です．必ず専用の充電器を使用してください．本電源は使用しないでください．

白色LEDの$V_F$/$I_F$特性の測定

白色LEDを使用したLED照明が普通に使われています．秋葉原には，白色LEDのジャンク部品が売っています．

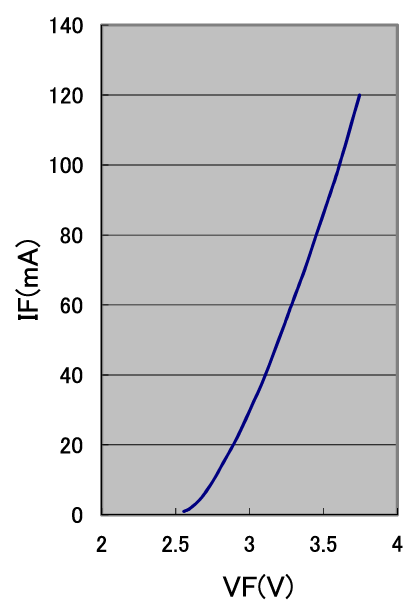
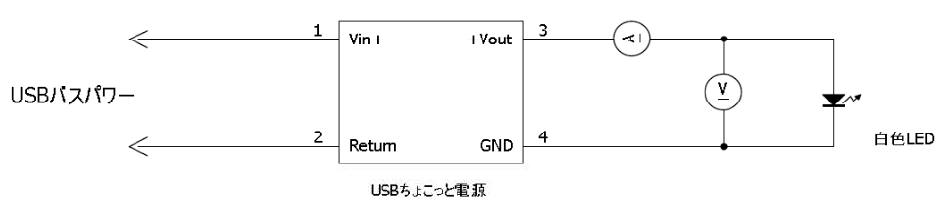
本電源を利用すれば，白色LEDの順方向電圧（$V_F$ ）特性を測定できます．LEDに電流を流してLEDの両端電圧を測定するだけです．

$V_F$特性をグラフにするので，低い電流値から少しずつ段階的に電流を増加させて，都度電圧を記録します．

図4に測定結果を示します．図5はその測定回路です．

電源の出力電圧は白色LEDの$V_F$より高くします．一般的な白色LEDの$V_F$は3～4Vなので，4～5Vに設定するとよいでしょう．

定電流で駆動してください．電源の出力電圧はLEDの$V_F$でクランプされるので，直列の制限抵抗は不要です．

その他考えられる応用例

回路の正常動作範囲確認

本電源のターゲットである試作回路への供給電圧（$V_{CC}$）を徐々に上げていき，動作開始電圧の確認ができます．逆に，$V_{CC}$を徐々に下げて行くことで正常に動作する電源電圧範囲を調べることができます．

24Vリレー回路の動作実験

リレー制御回路の多くは，24V電源を使っています．本電源は，出力24V時，80mAを供給できます．

12V，15V系電源のオーディオ・アンプ製作

12～15VのOPアンプを使った単電源動作のオーディオ・アンプの製作に使えます．

LED照明用電源

本電源は，約30V出力できるので，直列接続した白色LEDモジュールを駆動できます．

図6にLED点灯のようすを示します．

5V/1Aのスマートホン用USBアダプタを使うと，約2.4Wを取り出せるので，最大8本直列のLEDに最大100mAを供給できます．$V_F$=3.5Vとして8本で28Vです．

可変抵抗で，定電流値を変えることで調光が可能です．デスクトップ照明用なら明るさは十分です．

DC-DC変換方式の検討

DC-DC変換方式はさまざまです．今回の目的にどの方式が最適かを検討します．

バック・コンバータ（降圧チョッパ回路）

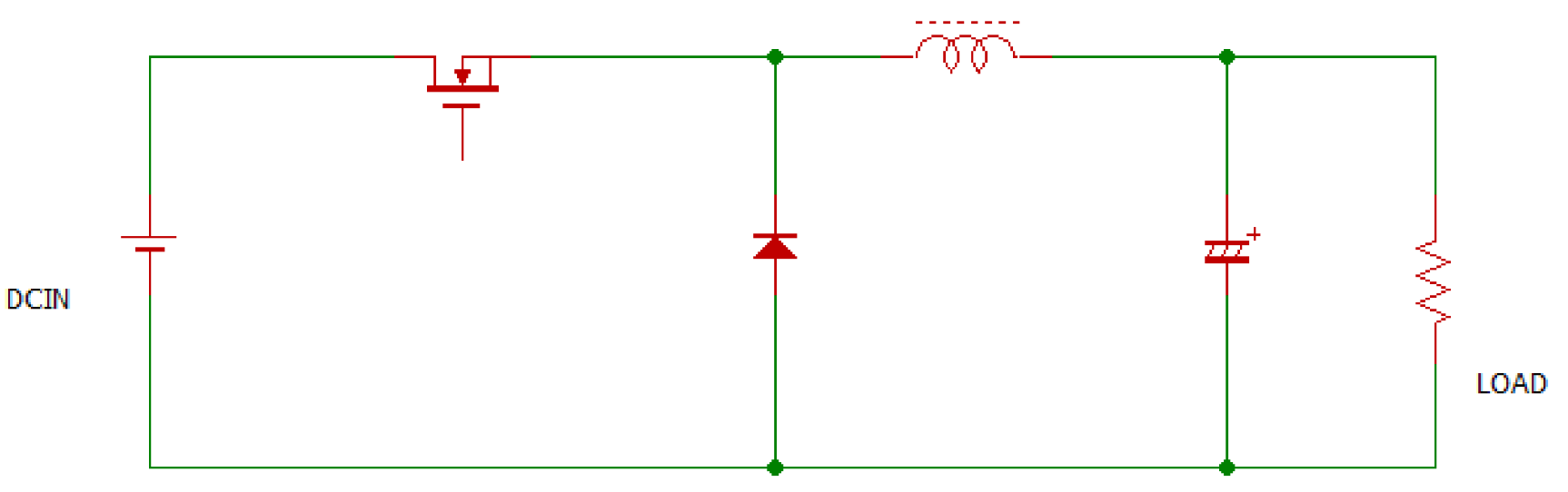
図7に基本回路を示します．もっとも広く使用されている回路方式です．入力電圧より高い電圧を出力することができないので，今回の用途には不向きです．

ブースト・コンバータ（昇圧チョッパ回路）

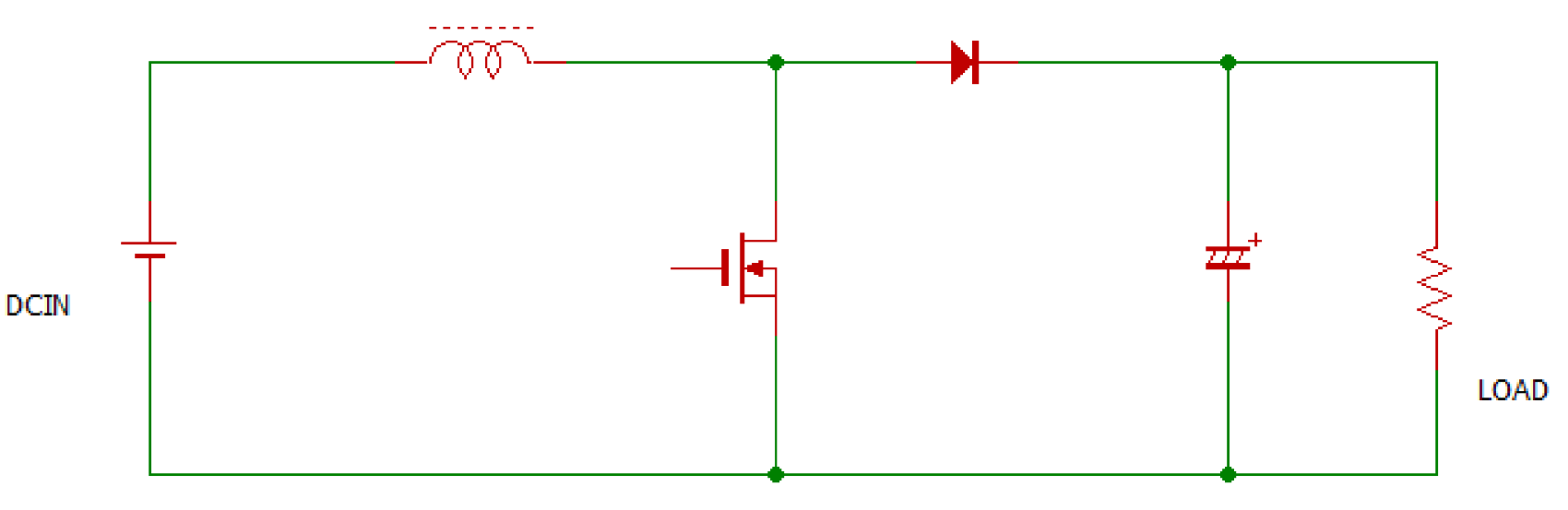
図8に基本回路を示します．入力より高い出力電圧がほしいときに便利な効率の高い電源回路です．入力電圧より低い電圧のときは，入力電圧が直接出力側に出てくるため，それより低い電圧を取り出すことはできません．出力が短絡されたとき，コンバータ回路の動作で保護することができないので，今回の用途には使用できません．

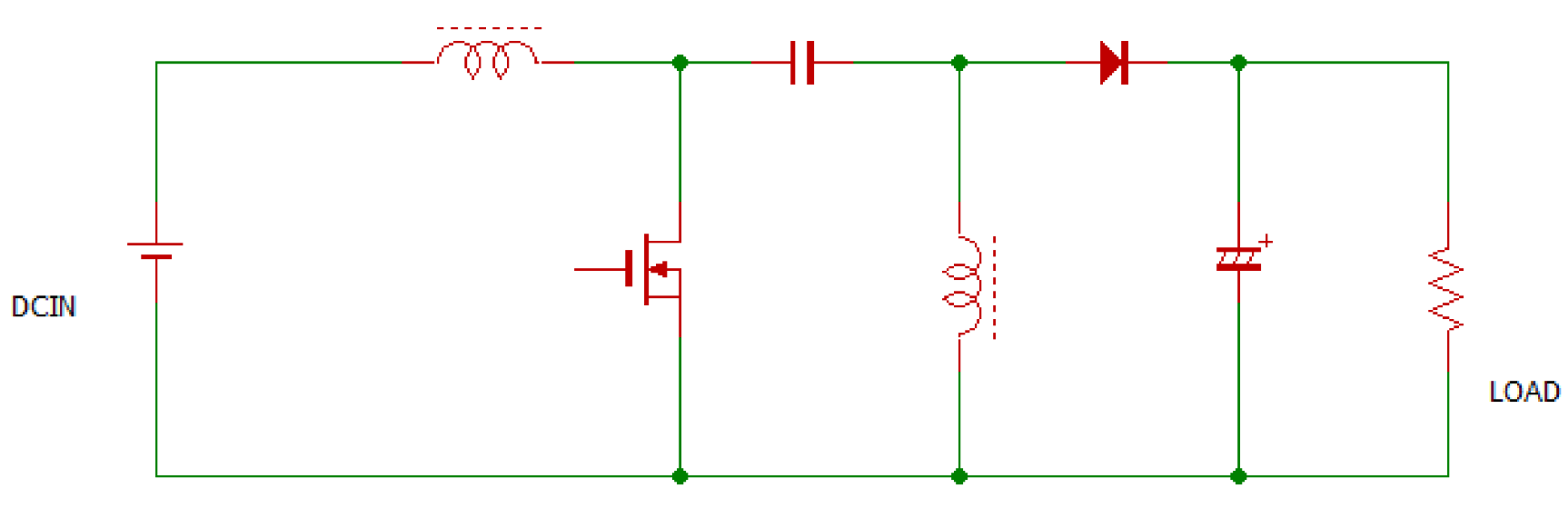
SEPICコンバータ（昇降圧コンバータ）

図9に基本回路を示します．

出力電圧は入力電圧より低くも高くもできます．チョーク・インダクタが2個＋カップリング・キャパシタが1個必要です．特殊なスイッチング・トランスが不要で，チョーク・インダクタで作ることができるので自作派向けでもあります．

出力電圧の可変範囲を広くすると，制御の安定性を確保できません．

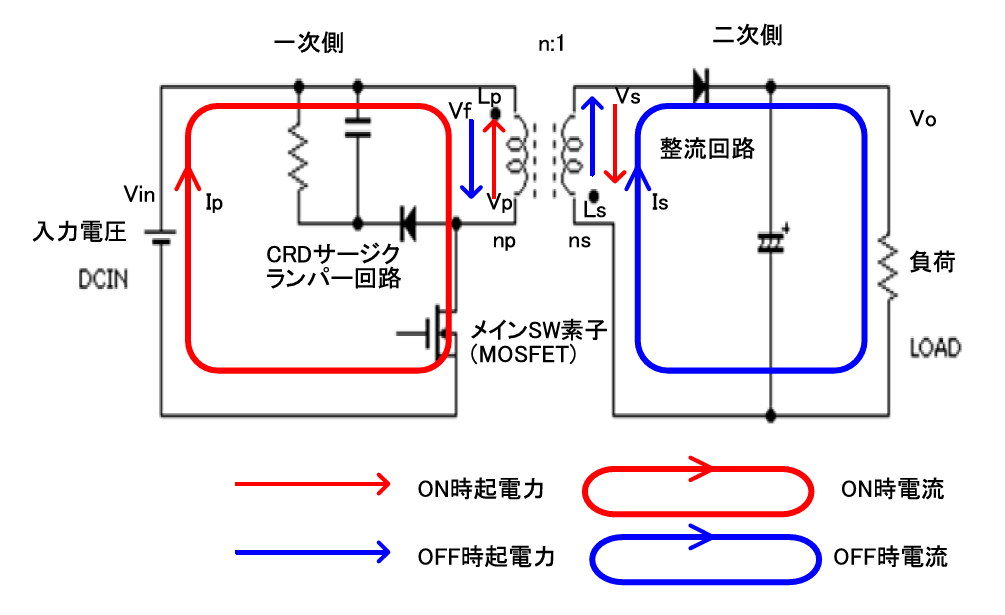
フォワード・コンバータ

図10に基本回路を示します．従来から，中高出力コンバータに使用されています．トランスを使いますが，基本はバック・コンバータと同じです．

メイン・スイッチがONのときに出力側にエネルギを供給します．整流回路にチョークが必要になるため，小出力電源にはコストや大きさの面で不利です．実際，市場でもほとんど利用されていません．

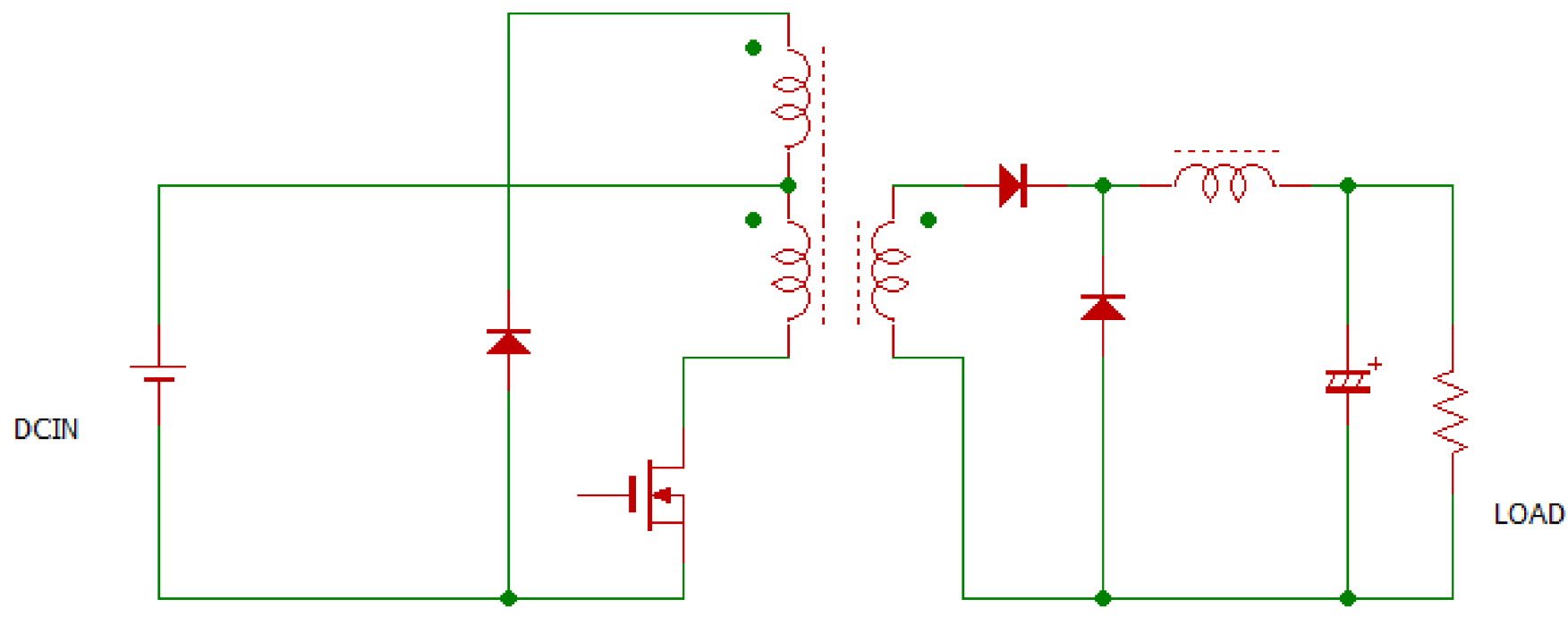
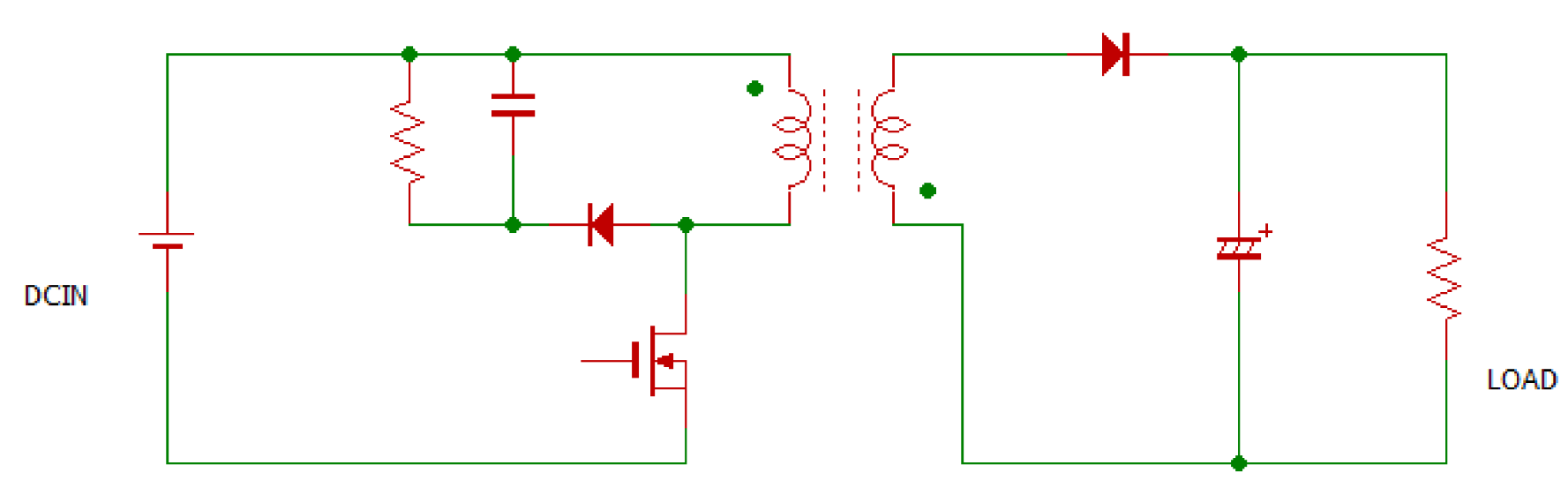
フライバック・コンバータの基礎

図11に基本回路を示します．

フォワード・コンバータと逆の動作をする電源です．メイン・スイッチがONのとき，トランスのインダクタンスにエネルギを溜めて，OFFのときに出力側にエネルギを放出します．

部品数が少なく回路が簡単です，市場に出ている電子機器に使用されている100W以下のスイッチング電源はほとんどこの方式を採用していると言って過言ではありません．

第2回　フライバック・コンバータの回路設計

オーソドックスなスイッチング電源「フライバック・コンバータ」

採用の理由

今回は，出力が3～24Vの広い範囲で，動作が安定するフライバック方式を採用します．

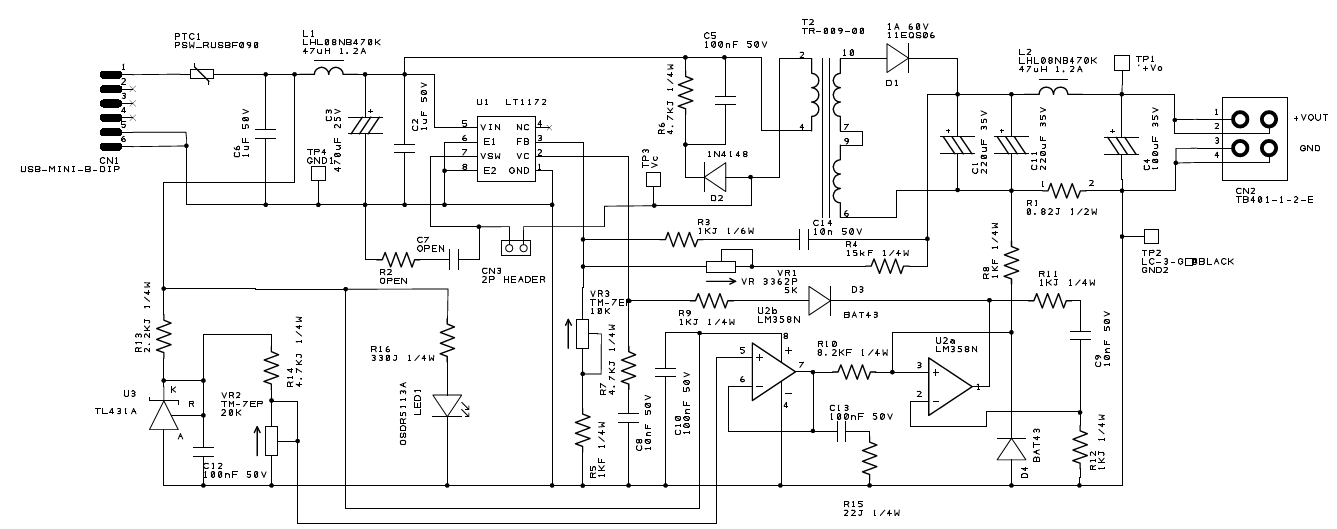
図12に製作したUSB電源の回路図を示します．表1は部品表です．

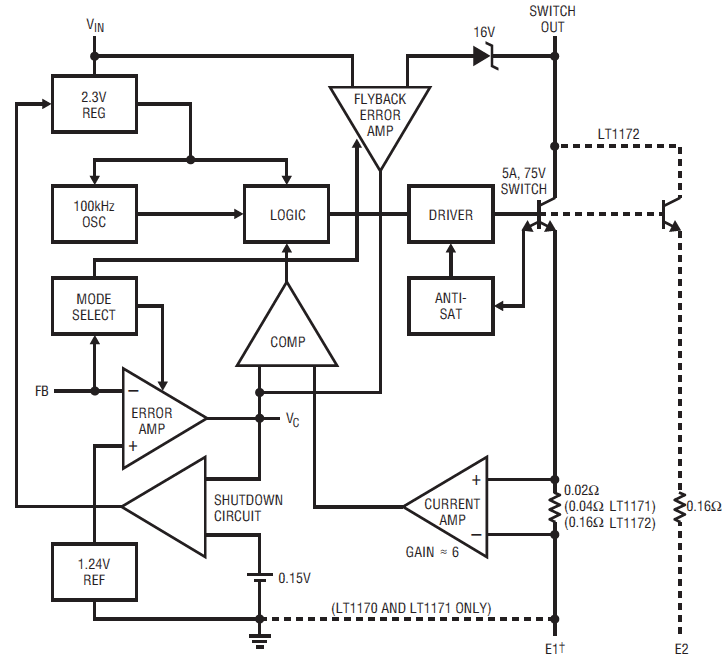
制御ICは，小型電源に最適なMOSFET内蔵のワンチップ電源IC LT1172CN8（アナログ・デバイセズ）を使います．パッケージはDIP-8で，出力5W程度のDC-DCコンバータに最適です．図13にLT1172の内部ブロック図を示します．

表1　USBプログラマブル電源の部品表

No	品名	Qty	仕様	メーカ/商社名	型名
--	プリント基板	1	CEM-3 t=1.6 35μ	友基	PC033-02
C1	電解キャパシタ	1	220μF 35V	RUBYCON	35ZLH220M8X11
C2	積層セラミック・キャパシタ	1	1μF 50V	MURATA	RDER71H105K2K1C03B
C3	電解キャパシタ	1	470μF 25V	RUBYCON	25PK470MEFC 8X11.5
C4	電解キャパシタ	1	100μF 35V	RUBYCON	35ZLH100M6.3X11
C5	積層セラミック・キャパシタ	1	100nF 50V	MURATA	RPER71H104K2K1A03B
C6	積層セラミック・キャパシタ	1	1μF 50V	MURATA	RDER71H105K2K1C03B
C7	未実装
C8	積層セラミック・キャパシタ	1	10nF 50V	MURATA	RPER71H103K2S1A03A
C9	積層セラミック・キャパシタ	1	10nF 50V	MURATA	RPER71H103K2S1A03A
C10	積層セラミック・キャパシタ	1	100nF 50V	MURATA	RPER71H104K2K1A03B
C11	電解キャパシタ	1	220μF 35V	RUBYCON	35ZLH220M8X11
C12	積層セラミック・キャパシタ	1	100nF 50V	MURATA	RPER71H104K2K1A03B
C13	積層セラミック・キャパシタ	1	100nF 50V	MURATA	RPER71H104K2K1A03B
C14	積層セラミック・キャパシタ	1	10nF 50V	MURATA	RPER71H103K2S1A03A
CN1	USBコネクタ	1	USB MINI B DIP	秋月電子通商	C-02235
CN2	ワンタッチ端子台	1	P-01404	秋月電子通商	TB401-1-2-E
CN3	ピン・ヘッダ	1	2P P2.54	秋月電子通商	C-00167（2Pにカット）
D2	小信号ダイオード	1	1N4148	FAIRCHILD	1N4148
D3	ショットキー・バリア・ダイオード	1	BAT43	ST-MICRO	BAT43
D4	ショットキー・バリア・ダイオード	1	BAT43	ST-MICRO	BAT43
L1	固定インダクタ	1	47μH 1.2A	TAIYO YUDEN	LHL08NB470K
L2	固定インダクタ	1	47μH 1.2A	TAIYO YUDEN	LHL08NB470K
PTC1	ポリスイッチ	1	16V 1.8A	LITTEL	RUSBF090
R1	酸化金属皮膜抵抗	1	0.82Ω 1/2W	PANASONIC OR 同等品	ERX12SJR82
R2	未実装
R3	カーボン被膜抵抗	1	1kΩ 1/4W	KOA OR 同等品	CFS1/4-102J
R4	カーボン被膜抵抗	1	15kΩ 1/4W	KOA OR 同等品	MFS1/4-1502F
R5	カーボン被膜抵抗	1	1kΩ 1/4W	KOA OR 同等品	MFS1/4-1001F
R6	カーボン被膜抵抗	1	4.7kΩ 1/4W	KOA OR 同等品	CFS1/4-S472J
R7	カーボン被膜抵抗	1	4.7kΩ 1/4W	KOA OR 同等品	CFS1/4-472J
R8	カーボン被膜抵抗	1	1kΩ 1/4W	KOA OR 同等品	MFS1/4-1001F
R9	カーボン被膜抵抗	1	100Ω 1/4W	KOA OR 同等品	CFS1/4-101J
R10	カーボン被膜抵抗	1	8.2kΩ 1/4W	KOA OR 同等品	MFS1/4-8201F
R11	カーボン被膜抵抗	1	1kΩ 1/4W	KOA OR 同等品	CFS1/4-102J
R12	カーボン被膜抵抗	1	1kΩ 1/4W	KOA OR 同等品	CFS1/4-102J
R13	カーボン被膜抵抗	1	2.2kΩ 1/4W	KOA OR 同等品	CFS1/4-222J
R14	カーボン被膜抵抗	1	4.7kΩ 1/4W	KOA OR 同等品	CFS1/4-472J
R15	カーボン被膜抵抗	1	22Ω 1/4W	KOA OR 同等品	CFS1/4-220J
R16	カーボン被膜抵抗	1	330Ω 1/4W	KOA OR 同等品	CFS1/4-331J
T2	スイッチング・トランス	1	EPC13 10P	シンセイ電機	TR-009-00
U1	IC	1	LT1172	Analog Devices	LT1172CN8
U2	IC	1	LM358N	FAIRCHILD	LM358N
U3	IC	1	Vref = 2.5V ±1%	TI	TL431A
LED1	LED		φ5 赤	秋月電子通商	OSDR5113A
VR1	可変抵抗	1	5kΩ	BOURNS	3296W-1-502
VR2	可変抵抗	1	20kΩ	COPAL	TM-7EP 20k
VR3	可変抵抗	1	10kΩ	COPAL	TM-7EP 10k
J	ジャンパ・ピン	1	P2.54 黒	秋月電子通商	P-03687
TP1	テスト・ピン	1	赤	マックエイト	LC-3-G 赤
TP2	テスト・ピン	1	黒	マックエイト	LC-3-G 黒
TP3	テスト・ピン	1	赤	マックエイト	LC-3-G 赤
TP4	テスト・ピン	1	黒	マックエイト	LC-3-G 黒
JP1	ジャンパ・ワイア	1	錫めっき銅線 φ0.6×10mm
JP2	ジャンパ・ワイア	1	錫めっき銅線 φ0.6×7.5mm
JP3	ジャンパ・ワイア	1	錫めっき銅線 φ0.6×7.5mm
JP4	ジャンパ・ワイア	1	錫めっき銅線 φ0.6×7.5mm
JP5	ジャンパ・ワイア	1	錫めっき銅線 φ0.6×5mm

製作した電源回路の動作

SW：ON後の動作

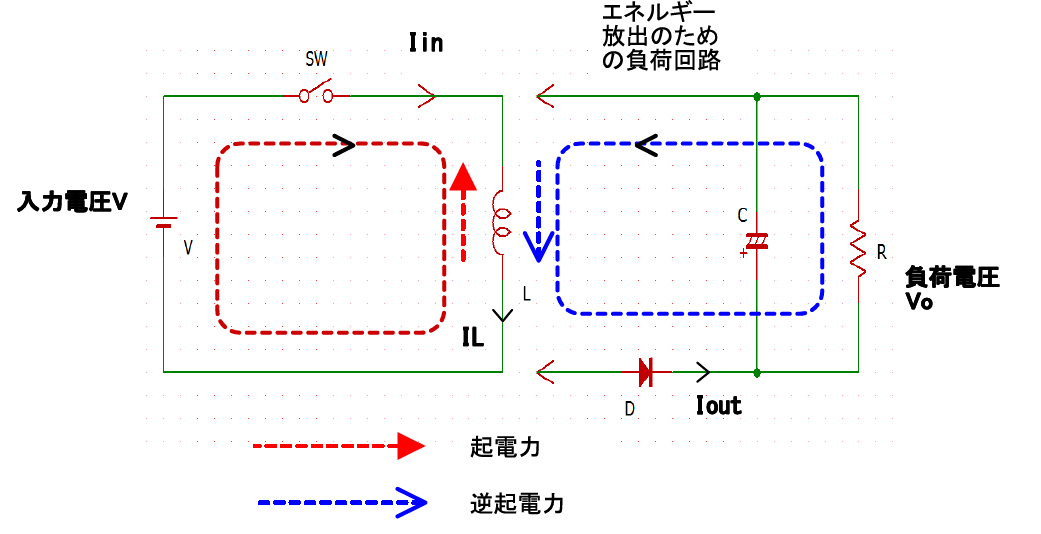
図14に，本電源が採用したフライバック方式の原理回路を示します．

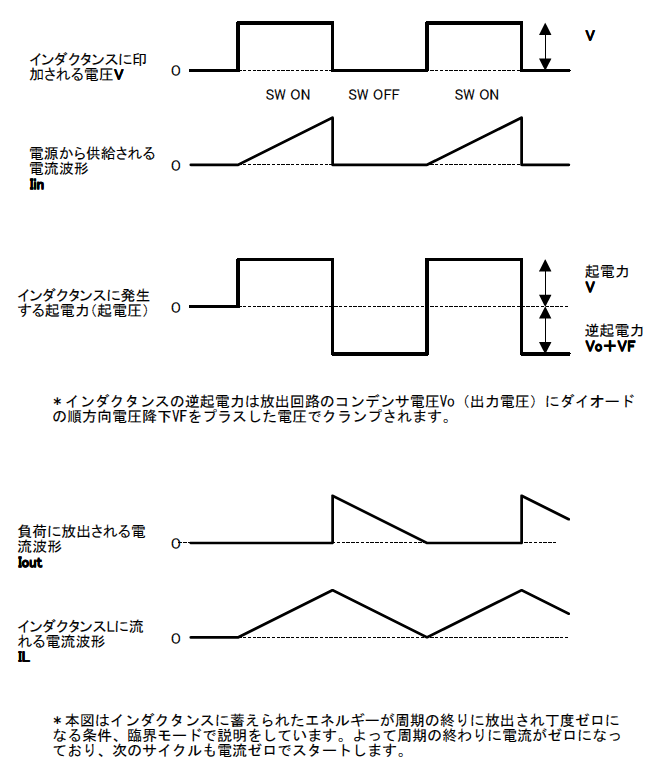
図15は，各部の電圧と電流の波形です．

SWをONにすると，インダクタンスに電流が流れ始めて時間とともに直線的に増します．

鉄心が飽和しない範囲では，電流の大きさ$\Delta I$は入力電圧を$V_{in}$，経過時間を$t$とすると次式で表されます．

\begin{align} \Delta I &= \dfrac{V_{in} \times t}{L} \end{align}

インダクタンス$L$が蓄えることのできるエネルギ$E$［J］は次式で表されます．

\begin{align} E &= \dfrac{1}{2} \times L \times (\Delta I)^2 \end{align}

時間$t$が経過した時点で，この計算で求まるエネルギがインダクタンスに蓄えられます．

SW：OFF後の動作

インダクタはキャパシタと違い，エネルギを保持できず，放出する性質をもっています．

インダクタには，流れていた電流を流し続けようとする性質がありますが，SWがOFFすると，インダクタを含む回路がオープン（開放）状態になり，電流を流し続けることができなくなります．

インダクタは手段を選ばず，とても大きな逆起電圧（フライバック電圧）を発生させて，その電圧はどんどん上昇して空気の絶縁を破り，火花放電を起こして，エネルギを放出します．

「フライバック」とは，インダクタンスの逆起電力の意味です．フライバック・コンバータの語源はここにあります．

この逆起電圧の火花放電を利用している応用製品として，ガス・コンロやガソリン・エンジン車の点火装置などがあります．

放電時のインダクタンス$L$の電圧と電流，時間の関係は，逆起電力を$V_{f}$，放電時間を$t_{discharge}$とすると次式で表されます．

\begin{align} \Delta I &= -\frac{V_{f} \times t_{discharge}}{L} \end{align}

SW OFF直前の$\Delta I$とインダクタンス$L$は不変ですから，放電時間を長くするか，電圧を高くすることで，この式のつじつまが合います．インダクタに低い電圧でクランプする回路を接続しておけば，時間をかけて（穏やかに）エネルギが放出されわけです．

フライバック・エネルギを消化する回路を追加

エネルギの放出回路を追加すると，インダクタから発生するフライバック・エネルギを制御できます．放出回路とは，ダイオード，キャパシタ，負荷抵抗で構成される整流回路です（図14）．

整流回路に放出されたSW OFF時のエネルギは，キャパシタで平滑されて，直流電圧が負荷抵抗に供給されます．

2次側電圧はSWのON時間で制御する

図16に示すのは，製作したUSB電源の基本回路と電圧/電流の流れです．

希望の出力電圧を得るためには，負荷で消費する電力と同じ電力がインダクタに蓄積されるように，メイン・スイッチのON時間を調整します．

つまり，フライバック・コンバータの2次側の出力電圧は，トランスの巻き線比に直接関係がなく決まります．1次側から供給されるエネルギと負荷で消費されるエネルギのバランスが取れるような出力電圧になるということです．

目標仕様を整理

本電源の心臓部はDC-DCコンバータ部です．第2回は，上記のコンセプトと仕様に基づいて，回路を設計します．表2に設計目標を示します．

表2　製作する実験用電源回路の仕様

項目	値など
入力電圧（Vin）	＋DC5.0V ±10%
出力電圧（Vout）	3～28V可変，最大3W（Pout）
スイッチング周波数	100kHz（使用IC：LT1172の動作周波数）
フライバック電圧の決定	（後述）

パワー部の設計

制御ICの内蔵トランジスタの耐圧を超えてはいけない

フライバック・コンバータのメイン・スイッチ部を設計します．

本電源回路が，その最大電圧28Vを出力するときに，制御IC LT1172の内蔵トランジスタの耐圧の65Vを超えてはいけません．

内蔵トランジスタには，次の3つの電圧の合計が加わります．

1. 入力電圧$V_{in}$
2. フライバック電圧$V_{f}$
3. サージ電圧$V_{surge}$

つまり，内蔵トランジスタに加わる電圧（$V_{DS}$）は次式で表されます．

\begin{align} V_{DS} &= V_{in} + V_{f} + V_{surge} \end{align}

フライバック電圧の上限を15Vに設定

フライバック電圧$V_{f}$は次のようになります．

\begin{align} V_{f} &= V_{DS} - V_{surge} - V_{in} \end{align}

$V_{surge}$は，スイッチング・トランスの1次-2次間の巻き線間の漏れインダクタンスに蓄えられたエネルギが2次側にエネルギを放出できず，1次側に戻されて生じます．その大きさは，後述のサージ・クランパ回路の設計で決まります．現時点では，$V_{surge}$=10Vと仮定します．

制御IC LT1172の内蔵トランジスタに加えることのできる最大電圧を$V_{DSmax}$とすると，許容できるフライバック電圧$V_{f}$は次のようになります．耐圧は，定格（65V）の80$\%$でディレーティングして計算します． \begin{align} V_{f} \le 65 \times 0.8 - 5 - 10 \le 37 \mathrm{V} \end{align}

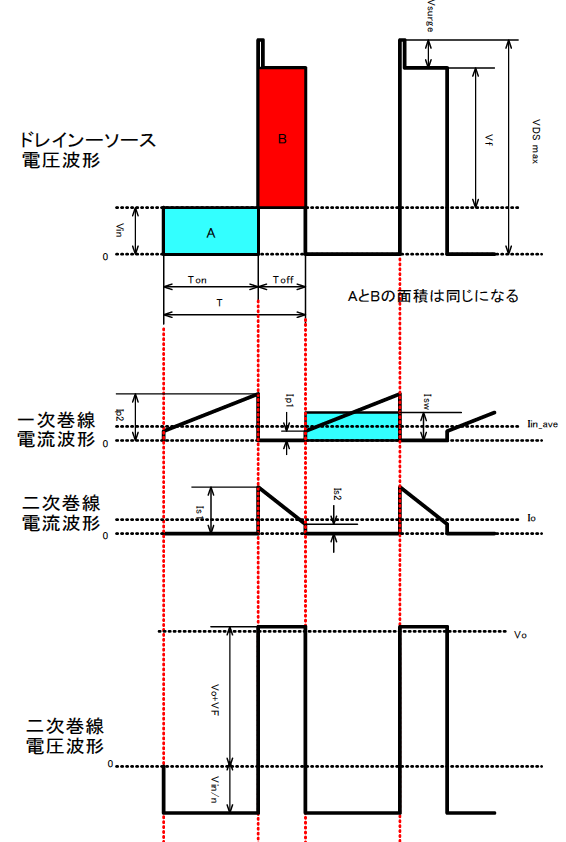
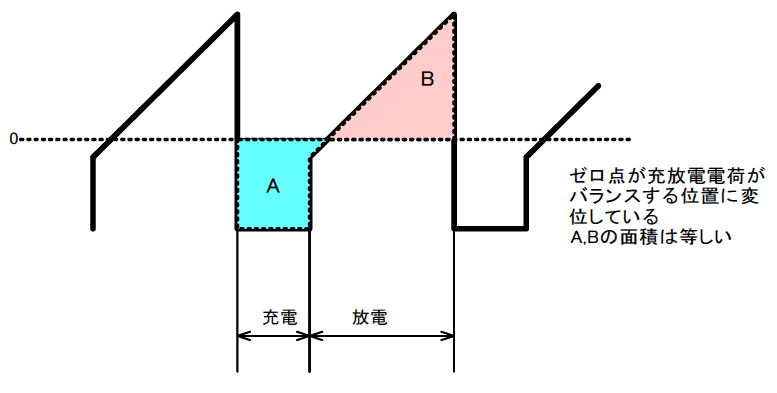
蓄えられたエネルギと放出されるエネルギは等しいので，入力電圧と内蔵トランジスタのON時間の積（$Vt$積）とフライバック電圧（$V_f$）と放電時間（OFF時間）の積（$Vt$積）は等しくなります（図17）．

制御IC LT1172が出力するゲート駆動信号のオン・デューティの最大値は85$\%$ですから，ON 時間は8.5$\mu$s（=周期10$\mu \times $0.85）です．

入力電圧の最低保証電圧は4.5Vなので，内蔵トランジスタがON時の$Vt$積は次のようになります．

\begin{align} 4.5 \mathrm{V} \times 8.5 \mu\mathrm{s} = 38.25 \mathrm{V}\mu s \end{align}

このときの内蔵トランジスタのOFF時間$T_{off}$は，スイッチング周期 $T=10\mu$sから$T_{on}=8.5\mu$sを引いた値 1.5$\mu$sです．

$Vt$積は同じなのでフライバック電圧$V_{f}$［V］は次のようになります．

\begin{align} V_{f} &= \dfrac{38.25 \mathrm{V}\mu s}{1.5 \mu\mathrm{s}} = 25.5 \mathrm{V} \end{align}

ディレーティングを80$\%$とすると37Vです．しかし，制御ICの制限があるため，25.3V以上になりません．

今回の電源の最大出力電圧目標は28Vなので，巻き線比 $N_S/N_P$を1：2にすると決めて，フライバック電圧 $V_f$が 15V（=30V $\times$ 0.5）になるように設計します．

内蔵トランジスタのON時間の最大値

本電源のトランスの1次-2次間の巻き線比 $n$ は次式で求めることができます．

\begin{align} n = \dfrac{V_{f}}{V_{\mathrm{Omax}} + V_{F}} = \dfrac{15 \mathrm{V}}{28 \mathrm{V} + 0.5 \mathrm{V}} = 0.526 \end{align}

整数倍になるようにしたいので，切り上げて巻き数比を0.5にします．すると，28V出力時の1次側のフライバック電圧$V_{f}$は，逆算で次のように求まります．

\begin{align} V_{f} = (28 \mathrm{V} + 0.5 \mathrm{V}) \times 0.5 = 14.25 \mathrm{V} \end{align}

このフライバック電圧$V_{f}$から，オン・デューティの最大値を求めます．ONとOFF時の$Vt$積は同じという原則から，次式が成立します．

\begin{align} V_{in} \times T_{on} = V_{out} \times T_{off} \end{align}

オン・デューティが最大になる最小入力電圧，最大出力のとき，つまり，$V_{f}$=14.25V，$V_{in}$=4.5Vのとき，ON時間$T_{on}$は次式から7.6$\mu$sと求まります．

\begin{align} T_{on} = T \times \left( \dfrac{1}{\dfrac{V_{in}}{V_{f}} + 1} \right) = 10 \mu\mathrm{s} \times \left( \dfrac{1}{\dfrac{4.5 \mathrm{V}}{14.25 \mathrm{V}} + 1} \right) = 7.6 \mu\mathrm{s} \end{align}

$T_{off}$は，スイッチング周期$T$から，$T_{on}$を引いた残りの時間になるため，次のように求まります．

\begin{align} T_{off} = T - T_{on} = 10 \mu\mathrm{s} - 7.6 \mu\mathrm{s} = 2.4 \mu\mathrm{s} \end{align}

入力電流と内蔵トランジスタの電流

内蔵トランジスタ，トランス，整流部の損失を考慮して，全体の電力変換効率を75$\

設計の初期では，損失に関わる電流や電圧の値がわからないため，経験上妥当な効率を仮定して計算を開始します．その結果から各損失を計算して，逆算で正確な効率を追い求めていきます．より正確な値が必要なら，補正された効率を使って，再度，各部の電圧や電流を計算します．このように補正計算を何回か繰り返すことで，より正確な結果を得ることができますが，今回は，そこまで厳密な計算は不要でしょう．

入力電圧$V_{in}$が最小の4.5Vのときの入力平均電流$I_{inave}$は次のとおりです．

\begin{align} I_{inave} = \dfrac{P_{in}}{V_{inmin}} = \dfrac{4 \mathrm{W}}{4.5 \mathrm{V}} = 0.888 \mathrm{A} \end{align}

図17に示すように，ON期間中の内蔵トランジスタに流れる電流の平均値$I_{swave}$は，入力電流と等しくなります．

ここで，オン・デューティ $D_{on}$は0.76（=$T_{on}/T$=7.6$\mu$s/10$\mu$s）なので，内蔵トランジスタに流れる台形波を矩形波近似した電流の波高値$I_{sw}$（図17）は次のとおりです．

\begin{align} I_{sw} &= \dfrac{I_{in}}{D_{on}} = \dfrac{0.888 \mathrm{A}}{0.76} = 1.1684\mathrm{A} \end{align}

連続モードで動かす

フライバック・コンバータの動かし方には，次の3種類あります．

1. 不連続モード（DCM）：1次巻き線電流が不連続的に流れる
2. 連続モード（CCM）：1次巻き線電流が連続的に流れる（図17）
3. 臨界モード（QRM）：連続と不連続のちょうど境目で動作する

採用した制御ICは，スイッチング周波数固定（100kHz）なので，臨界モードで動かすことはできません．

不連続モード制御は，内蔵トランジスタに流れるピーク電流が大きいです．たとえば，出力電圧を12Vに設定した時，出力が2Wのとき，内蔵トランジスタに流れるピーク電流が制御IC LTC1172の過電流リミッタが働く2.4A$_{\rm{typ}}$に達します．最大出力目標は3Wなので，不連続モード（DCM）は使えません．

また，不連続モード（DCM）は，エネルギ伝達動作の休止期間が多く，トランスの利用効率が高くありません．同じ出力で設計したとき，内蔵トランジスタに流れる電流の実効値が大きく，損失も大きくなります．

以上の理由から，本電源は連続モード（CCM）を選択しました．

第3回　トランス設計その1：1次側のインダクタンスと鉄心の選定

トランスが蓄えるべきエネルギ量

内蔵トランジスタのスイッチングとトランスに流れる電流のようす

前回説明したとおり，DC-DCコンバータの回路は，フライバック方式とし，連続モード（CCM）で動作させます．

この回路では，図17に示すように，内蔵トランジスタがONしたとき，トランスの1次巻き線に流れる電流は，1次側電流は，0Aからではなくある大きさから流れ始めます．内蔵トランジスタがOFFの期間に，トランスに蓄えられたエネルギが放出されきらず残っているからです．

2次側電流も，0Aまで低下しないうちに，1次側の内蔵トランジスタがONします．この残留電流が1次側ON時に引き継がれます．

1次側電流は，内蔵トランジスタがOFFするまで，直線的に増大します．

2次側巻き線とと1次側巻き線のアンペア・ターンは等しくなります．アンペア・ターンとは，巻き数と電流の積で，「起磁力」と呼ばれます．

1次インダクタンスに蓄えられるエネルギ量

トランスの1次インダクタンスは，内蔵トランジスタがONしている間の電流の増加分（エネルギ$E$）を蓄えます．

このON期間に蓄積されるエネルギ$E$［J］は次式で表されます．

\begin{align} E = \dfrac{1}{2} \times L_P \times \left( I_{P2}^2 - I_{P1}^2 \right) \end{align}

次のとおり，$P_{out}$［W］は，1サイクルのエネルギ$E$とスイッチング周波数$f_{sw}$の積です．

\begin{align} P_{out} &= E \times f_{sw} \end{align}

1次インダクタンス$L_P$の必要値

算出手順

必要なトランスの1次インダクタンスを求めます．

図17に示すように，1次側電流$I_{P1}$から最大値$I_{P2}$までの電流の変化分$\Delta I_{P}$を決定します．

一般的に，最小入力電圧かつ最大負荷の条件で，内蔵トランジスタに流れる電流（矩形波で近似）の波高値$I_{sw}$の50～100$\%$に設定します．

\begin{align} \Delta I_{P} = I_{sw} \times 0.8 = 1.1684 \times 0.8 = 0.9347 \end{align}

$T_{on}$は既知（7.6$\mu$s）なので（第2回参照），$\Delta I_{P}$が決まれば，1次インダクタンス$L_P$を次のように求めることができます．

\begin{align} L_P = \dfrac{V_{inmin} \times T_{on}}{\Delta I_P} = \dfrac{4.5 \mathrm{V} \times 7.6 \mu\mathrm{s}}{0.934 \mathrm{A}} = 36 \mu\mathrm{H} \end{align}

36$\mu$Hは中途半端なので，E12系列標準値の33$\mu$Hとし，この値で$\Delta I_{P}$を計算しなおすと，次のように求まります．

\begin{align} \Delta I_{P} = \dfrac{4.5 \times 7.6 \mu\mathrm{s}}{33 \mu\mathrm{H}} = 1.036 \mathrm{A} \end{align}

$L_P=33\mu$Hのとき，4Wを出力するために必要な1次巻き線電流$I_{P1}$と$I_{P2}$は次式で求まります．

\begin{align} I_{P1} = I_{sw} - \dfrac{\Delta I_{P}}{2} = 1.1684 \mathrm{A} - \dfrac{1.036 \mathrm{A}}{2} = 0.6504\mathrm{A} \end{align} \begin{align} I_{P2} = I_{sw} + \dfrac{\Delta I_{P}}{2} = 1.684 \mathrm{A} + \dfrac{1.036 \mathrm{A}}{2} = 1.6864 \mathrm{A} \end{align}

33$\mu$Hの1次インダクタンスで出力4Wを確保できることを確認

以上から，供給電力$P_{out}$を計算すると次のようになります．

\begin{align} P_{out} = \dfrac{1}{2} \times 33 \mu\mathrm{H} \times \left( (1.6864 \mathrm{A})^2 - (0.6504 \mathrm{A})^2 \right) \times 100 \mathrm{kHz} = 3.994 \mathrm{W} \end{align}

設定どおり，4Wを出力できることが確認できました．

コアを決める

4W出力に必要なコアのエネルギ蓄積容量$LI^2$を求める

トランスのコアの材料とサイズを検討します．

どんなコア製品も，扱えるエネルギ量（容量）に上限があり，そのコア製品を使って作るトランスのインダクタンスと巻き線に流す電流の最大値の2乗積 $LI^2$がその上限値を超えてはいけません．

今回の電源は1次インダクタンス$L_P$が33$\mu$H，最大4W出力時の最大電流1.686Aなので，$LI^2$積は次のように求まります．

\begin{align} L I^2 = 33 \mu\mathrm{H} \times (1.6864 \mathrm{A})^2 = 94 \times 10^{-6} \end{align}

製品カタログから$LI^2$値を計算する方法

コア・メーカの製品カタログには，$LI^2$値は掲載されていません．$LI^2$は，許容最大磁束密度，許容電流密度，鉄心の巻き線窓面積に占める導体の割合（巻き線の占積率）の各設定値で決まります．これらの値は，ユーザの都合で決まるため，カタログ値から自力で計算で求めるしかありません．

$LI^2$値を求める前に，下記の値を用意します．

1．製品カタログ値

1. 鉄心の有効断面積$A_E$［mm$^2$］
2. 標準ボビンの巻き枠の断面積［mm$^2$］：ボビン巻き高さ$\times$巻き幅

2．ユーザの使用条件

1. 最大磁束密度$B_{max}$［Gauss］：使用する鉄心の飽和磁束密度$\times$余裕率（80～90$\%$）
2. 銅線の単位断面積に流す電流の大きさ［A/mm$^2$］：数Wの小電力電源に使う小形鉄心の場合は8～10 A/mm$^2$，数十Wの中電力電源に使う中形鉄心では，5～8A/mm$^2$，100W以上の大電力電源に使う大形鉄心の場合は3～5A/mm$^2$です．

3. 巻き線の占積率（ボビンの巻き線窓面積に占める導体の割合）：機能的な低レベルの絶縁でよければ65～75$\%$，安全規格を満足する絶縁が必要なら50～65$\%$です．高い絶縁レベルを求めるほど占積率は低くなります．

LI$^2$の計算

ボビンに1ターンの銅線を巻くと仮定します．

まず，ボビンの巻き枠窓面積$\times$占積率から，導体の断面積を求めます．次に，電流密度$\times$断面積で銅線に流せる電流値$I$を計算します．

この電流$I$を1ターンの巻き線に流したときの磁束密度が最大になるインダクタンス$L$を次式で計算します．

\begin{align} L = \dfrac{B_{max} \times A_{E}}{I} \end{align}

ここで求まるインダクタンス$L$と電流$I$から，$LI^2$を求めます．

巻き線が1つしかないインダクタの場合は，この値をそのまま使いますが，今回のように1次と2次をもつトランスの場合はこの値の半分を$LI^2$とします．

フェライト・コア EPC13 PC40（TDK製）を検討

経験的に，フェライト・コアEPC13 PC40を第一候補として計算してみます．

EPC13の13はサイズを表し，コアの中央柱の直径や外形寸法を示しています．13は約13mmサイズのコアを意味します．PC40は材料を表します．TDKの資料によれば，高い飽和磁束密度（$B_{saturation}$=500mT），良好な損失特性（中～高周波向け），スイッチング周波数は25k～500kHzです．

EPC13の有効断面積は12.5mm$^2$です．巻き線窓面積は11.3mm$^2$です．

巻き線の占積率を60$\%$，電流密度を9A/mm$^2$とすると，巻き線に流せる電流$I$は，次式から61.02Aです．

\begin{align} I = 11.3 \mathrm{mm}^2 \times 0.6 \times \dfrac{9 \mathrm{A}}{\mathrm{mm}^2} = 61.02 \mathrm{A} \end{align}

EPC13 PC40の最大飽和磁束密度 $B_{max}$は3500gaussです．余裕率を90$\%$として3150gaussと考えます．61.02Aを流して，$B_{max}$が3150gaussになるインダクタンス$L$を求めると，次式から64.5nHです． \begin{align} L = 3150 \mathrm{gauss} \times \dfrac{12.5 \mathrm{mm}^2}{61.02 \mathrm{A}} = 0.0645 \mu\mathrm{H} \end{align}

このコアが蓄積できるエネルギ量$LI^2$は次式から240$ \times 10^{-6}$です．

\begin{align} L I^2 = 0.0645 \mu\mathrm{H} \times (61.02 \mathrm{A})^2 = 240 \times 10^{-6} \end{align}

今回のトランスは，1次と2次の2つの巻き線をもつため，必要なコアの蓄積容量はこの半分です．つまり，EPC13で作るトランスに蓄積できるエネルギ容量$LI^2$は，120$\times 10^{-6}$です．

4W出力に必要な94$\times 10^{-6}$に対して，余裕があり，十分使用可能です．

第4回　トランス設計その2：線材と巻き数の計算

1次巻き数の計算

1次巻き数$N_P$は，第3回で求めた必要1次インダクタンス$L_P$（33$\mu$H）と，1次電流の最大ピーク（1.6864A），鉄心の有効断面積（$A_E$），最大磁束密度（$B_{max}$）を使って次式で求まります．

\begin{align} N_{P} = \dfrac{L_P \times I_{peak}}{A_E \times B_{max}} \times 10^{8} \end{align}

各変数

上式の各変数は次のとおりです．

1次インダクタンス$L_P$

本連載第2回で，4W出力に必要な1次インダクタンス$L_P$を求めました．その値は33$\mu$Hです．

コアの有効断面積$A_E$

EPC13サイズの有効断面積$A_E$は0.125cm$^2$です．

コアの最大磁束変化幅 $\Delta B_{max}$

まず，本電源のトランスの使用温度を想定します．想定される最高周囲温度は40℃とします．

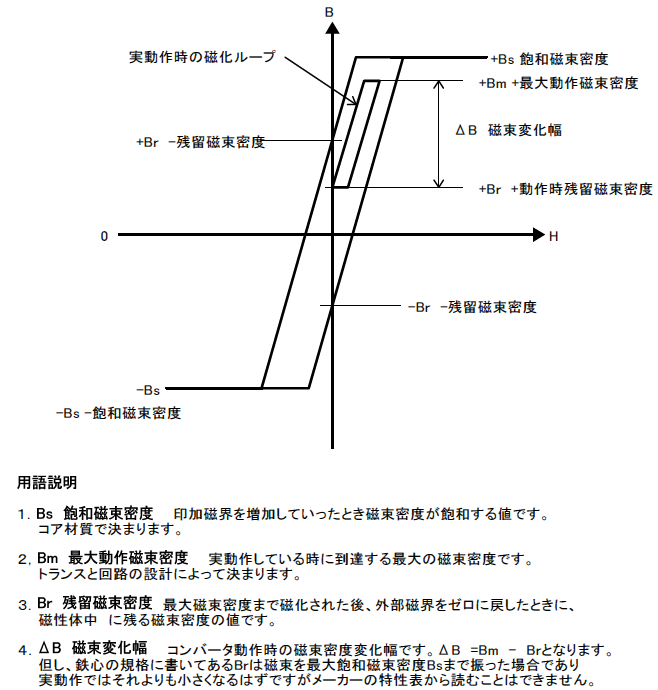
図18に，コアの$B-H$特性とフライバック・コンバータの実動作時の磁化曲線を示します．

EPC13サイズのコアは小形です．トランスの温度上昇を最大20℃まで許容すると，上限温度は60℃です．PC40材（TDK製）の60℃時の飽和磁束密度 $B_{saturation}$は，450mT（4500gauss）ですから，残留磁束密度$B_{residual}$は65mT（650gauss)です．

余裕率80$\%$としたとき，最大磁束密度は450mT $\times$ 0.8 = 360mTです．ここから$B_{residual}$の65mTを差し引くと次のようになります．

\begin{equation} \Delta B_{max} = 360\,\mathrm{mT} - 65\,\mathrm{mT} = 295\,\mathrm{mT}\,(2950\,\mathrm{gauss}) \end{equation}

ここで，$B_{residual}$=65mTとしていますが，この値は，飽和するまで磁束密度を大きく振って，磁界を 0 にしたときの値です．実際は65mTより小さいと想定できます．

1次側電流のピーク値

今回の電源で使用する制御IC LT1172Cの制限電流はカタログより2.4A$_{\rm{typ}}$です．この電流を1次最大ピーク電流とします．

上記の変数を式に代入すると次のように求まります．

\begin{align} N_{P} = \dfrac{33 \mu\mathrm{H} \times 2.4\mathrm{A}}{A_E \times \Delta B_{max}} \times 10^{8} = 21.5［ターン］ \end{align}

計算値は21.5ターンですが，切りよく20ターンとしました．

起動時や回路が急激な負荷変動があったときの磁束密度

定格3W出力時の1次側電流のピーク値は1.6864Aです．通常運転時の磁束密度は，2213gaussなので，最大磁束変動幅$\Delta B$の設計値である295mT（2950gauss)に対して余裕があります．

電源投入後，定常状態に達するまでの異常期間や，急激で大幅な負荷変動がある期間は，電流検出エラー・アンプからICのVC端子を制御するフィードバック・ループ系の遅れによって，1次電流が制御ICの電流リミット値に達する可能性があります．通常の動作ではこの電流制限に引っ掛る前にVC端子を制御する電流フィードバック系で制限されてしまうので，この電流に達することはありません．

制御IC LT1172のリミッタ電流がばらついたときの挙動

今回採用した制御IC LT1172の電流リミット値はばらつき幅が大きく，最小1.25A，標準2.4A，最大3.5Aです．出力28V/3W時の1次電流は1.6864Aですから，リミット値が1.25Aの制御ICをつかんでしまった場合，3Wを得ることができません．

逆にリミットがばらつき最大の3.5Aの制御ICをつかんだ場合は，過渡的な負荷時にコアが飽和領域に入る可能性があります．ただし，飽和して過電流が流れたとしても，制御IC LT1172には内蔵トランジスタを過電流破壊から保護するパルス・バイ・パルス過電流保護回路が内蔵されているので，問題ないでしょう．

この実験用電源は，制御IC LT1172の電流リミットがスペックほどはばらつかないだろうという希望的観測の元で設計しています．量産する場合は，出荷検査をして，最大出力が3W未満の製品を不良判定する必要があるでしょう．

2次巻き数の計算

1次巻き数$N_P$は20ターンと決まりました．

本電源のトランスの巻き線比は1：2と決めました（第2回）．したがって2次巻き数$N_S$は，次式から40ターン（=2 $\times$ 20ターン）です．

巻き線の線径の決定

1次電流と2次電流の電流実効値計算

トランスの巻き線に流れる電流から使用するエナメル電線の直径を見積もります．

図17に示すように，1次巻き線と2次巻き線に流れる電流は，矩形波に三角波が乗った形をしています．このような波形の電流の実効値$I_{RMS}$は次のような式を使うことで計算できます．

\begin{align} I_{RMS} = \sqrt{\dfrac{D_{on}}{3} \times \left( I_1^2 + I_2^2 + I_1 \times I_2 \right) } \end{align}

この式を使うと，1次巻き線の電流の実効値$I_{PRMS}$は次のように求まります．

\begin{align} I_{PRMS} &= \sqrt{ \dfrac{0.76}{3} \times \left(1.6864^2 + 0.6504^2 + 1.6864 \times 0.6504\right) } = 1.496 \mathrm{A_{RMS}} \end{align}

2次側の開始電流$I_{S1}$と終止電流$I_{S2}$は，1次側電流とアンペア・ターン（$AT$）が等しいという原則から，次のように求まります．

\begin{align} I_{S1} = I_{P2} \times n = 1.6864 \times 0.5 = 0.8432\,\mathrm{A} \\ I_{S2} = I_{P1} \times n = 0.6504 \times 0.5 = 0.3252 \mathrm{A} \end{align}

オフ・デューティが0.24なので，2次側電流の実効値$I_{SRMS}$は次式のように求まります．

\begin{align} I_{PRMS} = \sqrt{ \dfrac{0.24}{3} \times \left(0.8432^2 + 0.3252^2 + 0.8432 \times 0.3252\right) } = 0.6609 \mathrm{A_{RMS}} \end{align}

巻き線に流れる電流密度$\sigma$を8A/mm$^2$と仮定すると，1次と2次の巻き線に必要な電線の断面積$S$は次のように求まります．

\begin{align} S_{P} = \dfrac{I_{PRMS}}{\sigma} = \dfrac{1.496}{8} = 0.187 \mathrm{mm}^2 \end{align} \begin{align} S_{S} = \dfrac{I_{SRMS}}{\sigma} = \dfrac{0.6609}{8} = 0.0826 \mathrm{mm}^2 \end{align}

断面積から電線の直径を計算できます．各々の電線径$D$は次のとおりです．

\begin{align} D_{P} = \sqrt{\dfrac{0.187 \times 4}{3.14}} = 0.488\,\mathrm{mm} \end{align} \begin{align} D_{S} &= \sqrt{\dfrac{0.0826 \times 4}{3.14}} = 0.324 \mathrm{mm} \end{align}

ボビン幅にぴったりはまる線径

1次側と2次側の巻き線の結合が悪いフライバック・コンバータは，漏洩インダクタンスが大きく，1次側に発生するサージ電圧が増えて損失が大きくなり効率を悪くします．

結合度を高めるポイントは次の2つです．

1. 両者の巻き幅が等しく，巻き線の高さと巻き幅の比が大きい
2. 両巻き線を挟みこむサンドイッチ構造にする

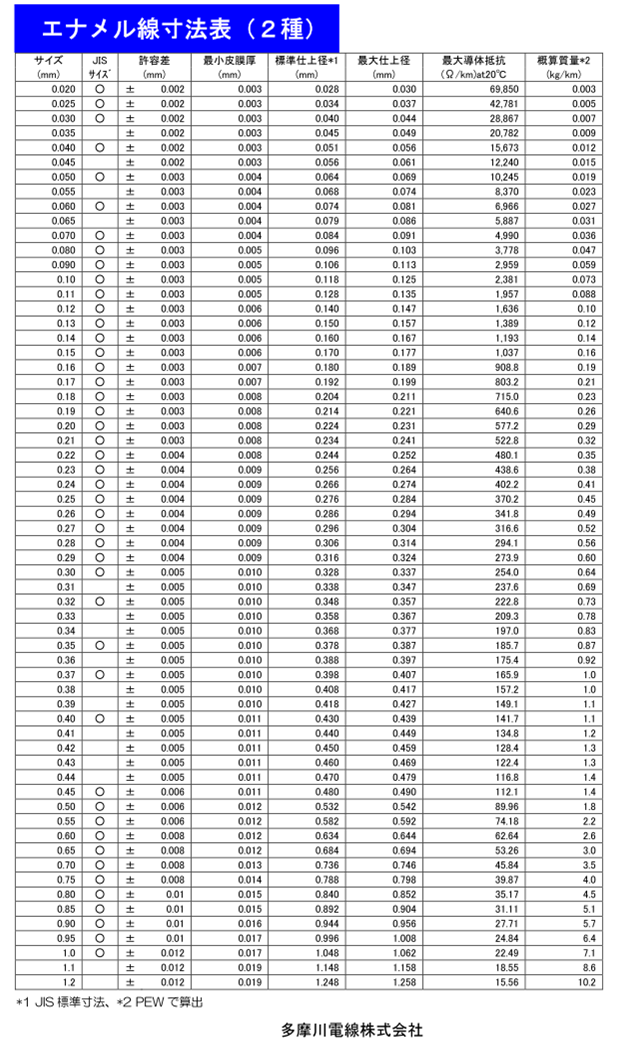
ポリウレタン・エナメル線を使って，ボビン幅いっぱいにきっちり巻ける線径を選びます．

EPC13サイズのコア用ボビンの巻き幅は，カタログから6.88mmです．この幅を目いっぱい使って，ぴったり20ターン巻き切るためには，線径は0.344mm（=6.88/20）が最適と計算できます．

図19に示すポリウレタン・エナメル線（多摩川電線）のカタログを参照すると，最大仕上径0.344mm以下で，かつ一番近いのは，$\phi$0.29の電線（最大仕上径は0.324mm）です．最大仕上径0.344mm以上の電線を選ぶと，ボビンに巻ききれなくなります．

2次側は$\phi$0.29の電線を20ターンを直列に巻きます．

1次側は，同じ$\phi$0.29の電線を2本並列にして巻き線します．2本まとめたときの線径は，$\phi$0.41（$=\phi 0.29 \times \sqrt{2}$）相当になります．予定の線径は0.488mmですが，こちらも多少細くなってしまいました．0.488mm径の許容電流密度は11.34A/mm$^2$です．EPC13は小さいコアなので，この程度の電流密度なら温度上昇は問題ないと判断して試作に進むことにしました．

トランスの仕様の整理

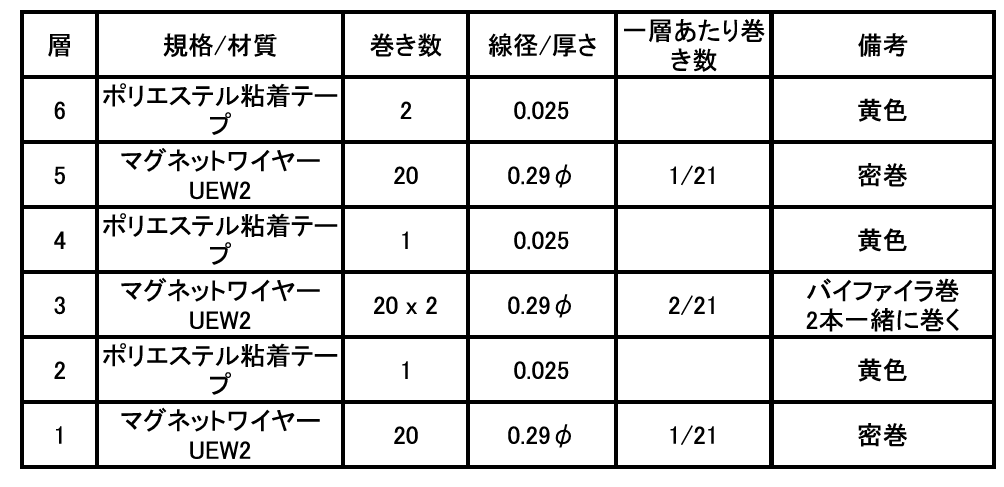
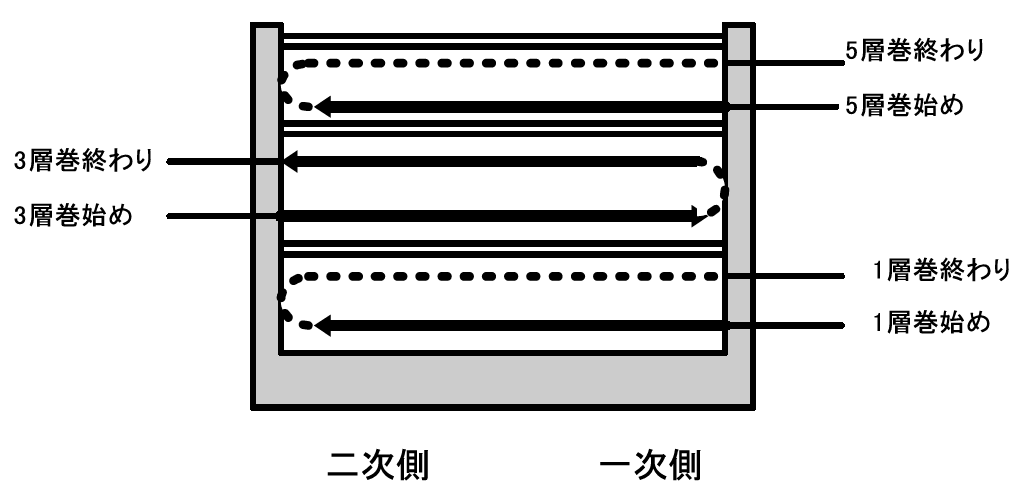
最終的にトランスの巻き線仕様は次のようになりました．図20に巻き線の順番を示します．

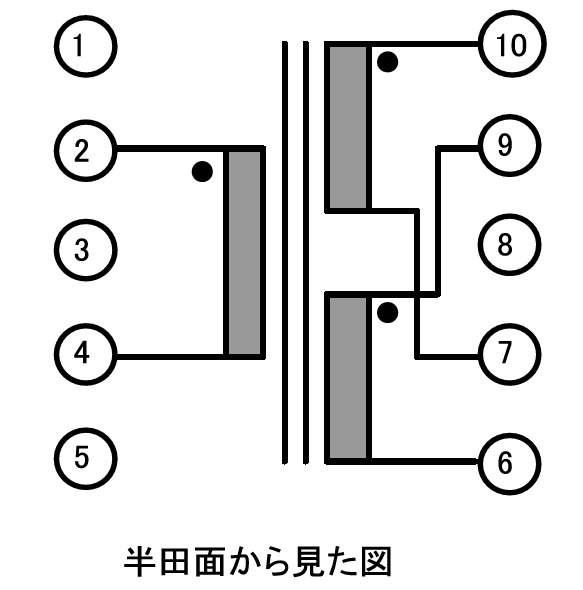
図21は巻き線の引き出し方向です．図22は結線図です．

1. 1次巻き線：20ターン，$\phi$0.29，ポリウレタン・エナメル線2本パラ
2. 2次巻き線：20ターン，$\phi$0.29，ポリウレタン・エナメル線，直列，計40ターン
3. 1次インダクタンス：33$\mu$H±10$\%$

巻き線構造は，1次巻き線を2次巻き線の半分で挟むサンドイッチ構造とします．

第5回　入出力回路と制御回路の設計

主回路部の設計が終わったら，入出力部と制御部の設計に移ります．図23に本器の回路図を再度掲載します．

入力部

ポリスイッチ

入力電源は，USBコネクタから+5Vが供給されます．

負荷回路の故障による過電流が発生した際，出力を遮断する定格電流0.9Aのポリスイッチを電源回路の正電源出力側に入れます．ポリスイッチは，高分子材料（ポリマ）を使った復帰型のヒューズです．

一般的なUSBポートが供給できるのは，500mAまた0mAですから，ポリスイッチは作動しませんが，大容量のACアダプタや出力電流制限のないUSBポートを備えるパソコンと組み合わせて使う場合に備えて，ポリスイッチを追加します．

リプル除去用の$LC$フィルタ

ポリスイッチの後段には，入力のリプル電圧と電流を減らす，$LC$フィルタ（$C_6$と$L_1$）を挿入します．カットオフ周波数（$f_C$）は，スイッチングより十分低い周波数に設定します．

カットオフ周波数$f_C$は次式で求まります．$C_1$は220$\mu$F，$L_1$は47$\mu$Hとしました．

\begin{align} f_C = \dfrac{1}{2 \times 3.14 \times \sqrt{220 \mu\mathrm{F} \times 47 \mu\mathrm{H}}} = 1565 \mathrm{kHz} \end{align}

瞬間的な負荷電流を供給する2個のキャパシタ

$LC$フィルタの後段には，DC-DCコンバータの瞬間的なパルス電流を供給するバイパス・キャパシタ$C_2$と$C_3$を追加します．

$C_3$には低周波成分の供給に適した電解キャパシタを，$C_2$には高周波数成分の供給に適した積層セラミック・キャパシタを使います．

このキャパシタがないと，DC-DCコンバータに流れ込む高い周波数のノイズ成分が入力ケーブルを通じて，パソコンの内部に侵入し，動作に悪影響を与える可能性があります．また，DC-DCコンバータ自体の動作も不安定になる原因になります．

図24に示すように，これらの入力キャパシタに流れるリプル電流は，1次巻き線電流と同じ波形です．

その実効値は次式で計算できます．

\begin{align} I_{\mathrm{RCin}} = \sqrt{ \dfrac{D_{on}}{12} \times \left(4 - 3 D_{on} \right) \times \left( I_{P1}^2 + I_{P2}^2 + I_{P1} \times I_{P2} \times \dfrac{4 - 6 D_{on}}{4 - 3 D_{on}} \right) } \end{align}

実用的には，そこまで正確に計算する必要はなく，1次電流を矩形波近似した$I_{sw}$で計算しても大差はありません

\begin{align} I_{RCin} &= I_{sw} \times \sqrt{D_{on} \times (1 - D_{on})} \\ &= 1.1684 \times \sqrt{0.76 \times (1 - 0.76)} \\ &= 0.499\,\mathrm{A_{RMS}} \end{align}

1次側のキャパシタには，100kHzでの許容リプル電流が0.499A以上の製品を選びます．PKシリーズ470$\mu$F/25V（ルビコン）は，100kHzにおけるリプル電流が660mA$_{\rm{RMS}}$なので十分な性能をもちます．

サージ吸収とノイズ対策

クランプ回路

トランスの漏れインダクタンスに蓄えられたエネルギは入力側に戻り，制御ICの内蔵トランジスタのドレインに加わります．このノイズを「サージ」と呼びます．

トランスの1次側巻き線は，5Vと制御ICのVSWピンに接続します．1次巻き線間に接続したD$_2$，$R_6$，$C_5$で構成する回路は，制御ICの内蔵トランジスタがOFFしたときに，トランスの漏洩インダクタンスによって生じるサージを吸収し，VSW端子の電圧を制御ICの許容電圧（65V）以下に収めます．

この対策回路を一般に「スナバ」と呼びますが，私はその働きを表す「サージ・クランパ」と呼んでいます．

具体的には，ドレイン側にダイオード D$_2$を接続して，$R_6$と$C_5$を組み合わせた回路に接続します．漏れインダクタンスから発生するエネルギをいったんキャパシタ（$C_5$）に蓄えて，抵抗（$R_6$）で熱に変換して消費します．この対策がないと，内蔵トランジスタに，耐圧を超える電圧が加わって壊れます．

漏洩インダクタンスに蓄えられるエネルギ（$P_{leak}$）は，次式で求められます．漏洩インダクタンス（$L_{leak}$）を1次インダクタンスの1.5$\%$と仮定します．つまり，0.495$\mu$H（=33$\mu$H$\times$0.015）として計算します． \begin{align} P_{leak} &= \dfrac{1}{2} \times L_{leak} \times I_{Ppeak}^2 \times f_{sw} \\ &= \dfrac{1}{2} \times 0.495\,\mu\mathrm{H} \times (1.6864)^2 \times 100\,\mathrm{kHz} \\ &= 0.0703\,\mathrm{W} \end{align}

厳密には，この電力以外にダイオードD$_2$が導通している期間に，2次側に放出するエネルギの一部がクランパ回路にも供給されるため，上式の計算結果より少し多くなります．計算が複雑になるので，この値を参考に余裕をもった定数設定をすればよいでしょう．

クランプ電圧（$V_{clamp}$）は，サージ電圧（$V_{surge}$）を10V$_{\rm{max}}$としたので，$V_{f}$（14.25V）を加えて，24.25Vです．

エネルギ消化用の抵抗の値（$R_{clamp}$）は，抵抗の消費電力が漏れインダクタンスから生じるサージ電力（$P_{surge}$）の0.0703Wとバランスするように設定します．次式で計算できます．

\begin{align} R_{clamp} = \dfrac{V_{clamp}^2}{P_{surge}} = \dfrac{24.25^2}{0.0703} = 14592 \Omega \end{align}

この値を参考に余裕をみて，E12系列の抵抗値6.8k$\Omega$，1/6Wとしました．

漏洩インダクタンスはトランスの作り方に依存し，仮定したとおりにはならないことも多いので，試作したら必ずリーケージ・インダクタンスを測定して確認します．

クランプ・キャパシタ（$C_{clamp}$）の容量は，$R_{clamp}$と$C_{clamp}$で計算した時定数が，スイッチング周期（10$\mu$s）の数倍以上になるように選びます．$C_{clamp}$=100nF，$R_{clamp}$=6.8k$\Omega$のときの時定数は680$\mu$sで，スイッチング周期（10$\mu$s）より十分大きいです．容量が不足していると，サージ電流が流れ込んだ際，充電電圧が一時的に上昇し，クランプ電圧が計算値より高くなります．

スイッチング・ノイズを低減する「スナバ」

制御IC LTC1172のVSW端子とグラウンドの間に接続した$C_7$と$R_2$は，スイッチング時の電圧の上昇速度（$\Delta V/\Delta t$）を遅くし，スイッチング・ノイズを低減する対策回路です．「スナバ」と呼びます．

キャパシタの容量を大きするほど，ノイズの抑圧効果が増しますが，損失も増えます．実際の波形を見ながら，定数を決めます．

スナバ・キャパシタ（$C_{snab}$）が220pFのときのスナバ抵抗の損失$P_{loss}$［W］は，次のように求まります．

\begin{equation} \begin{aligned} P_{loss} &= \dfrac{1}{2} \times C_{snab} \times \left( V_{in} + V_{f} \right)^2 \times f_{sw} \\ &= \dfrac{1}{2} \times 220\,\mathrm{pF} \times (4.5 + 14.25)^2 \times 100\,\mathrm{kHz} \\ &= 0.0038\,\mathrm{W} \end{aligned} \end{equation}

220pFでは，$P_{loss}$は非常に小さく，効果が限定的ですから，容量を大きくしたほうがよさそうです．最終的には効果を見ながら調整が必要です．今回は，試作後の動作確認において，スナバ回路がなくても十分サージ電圧が低いことが確認されたため非実装としました．

2次整流回路

2次側巻き線には，ショットキー・バリア・ダイオードD$_1$と電解キャパシタ$C_1$，$C_{11}$で構成した整流回路を接続します．2次巻き線の出力を平滑して直流に変換します．

ショットキー・バリア・ダイオードは，順方向電圧が低く，リカバリ電流のないので，ロスが小さくノイズの発生も小さいからです．

耐圧には留意が必要です．ダイオードに必要な耐圧（$V_{Rmax}$）は，入力最大かつ出力最大の条件で次式で求まります．

\begin{align} V_{R\max} = \dfrac{V_{inmax}}{n} + V_{out} = \dfrac{5.5 \mathrm{V}}{0.5} + 28 \mathrm{V} = 39\,\mathrm{V} \end{align}

耐圧39V以上で，電流定格が最大定格出力電流（0.3A）以上の製品を選びます．ここでは，1S6（1A，60V，PANJIT製）を選びました．

平滑用には，容量の大きい電解キャパシタを使います．許容リプル電流に留意する必要があります．平滑キャパシタに流れるリプル電流（$I_{RCout}$）は．1次入力キャパシタのときと同じく，次式で求まります．

\begin{align} I_{RCout} &= \sqrt{ \dfrac{D_{off}}{12} \times \left(4 - 3 D_{off}\right) \times \left( I_{S1}^2 + I_{S2}^2 + I_{S1} \times I_{S2} \times \dfrac{4 - 6 D_{off}}{4 - 3 D_{off}} \right) } \end{align}

電流波形を矩形波で近似して計算してもOKです．

本電源の出力電流（$I_{out}$）は最大0.3Aで，このときのオフ・デューティは0.24，2次電流の波高値（$I_{Ssw}$）は1.25A（=0.3/0.24）ですから，キャパシタのリプル電流（$I_{RCout}$）は次式で求まります．

\begin{align} I_{RCout} &= \sqrt{ \dfrac{D_{off}}{12} \times \left(4 - 3 D_{off}\right) \times \left( I_{S1}^2 + I_{S2}^2 + I_{S1} \times I_{S2} \times \dfrac{4 - 6 D_{off}}{4 - 3 D_{off}} \right) } \end{align}

今回は，ZLHシリーズ（ルビコン製）の220$\mu$Fを2本，並列で接続します．35V印加時の100kHzリプル電流の定格は950mAですから，余裕があります．

出力リプル・フィルタ

その後段には，$L_2$と$C_4$で構成したリプル・フィルタを挿入します．

出力される100kHzのスイッチングによるリプル電圧を抑圧して，変動の小さい直流を得ます．

カットオフは，100kHzより十分低い周波数に設定します．カットオフ周波数は次式で求まります．

\begin{align} f_{C} = \dfrac{1}{2 \times 3.14 \times \sqrt{100 \mu\mathrm{F} \times 47 \mu\mathrm{H}}}= 2322 \mathrm{Hz} \end{align}

十分低いのでOKです．

出力電圧帰還回路

出力電圧の$R_4+VR_1$と $VR_3+R_5$の分圧を制御IC LT1172のFB端子に入力します（図23）．

LT1172は，FB端子の電圧が，1.244V一定になるように出力電圧を制御します．$VR_3$では大まかに，$VR_1$では細かく出力電圧を調整します．

出力電圧$V_{out}$は次式で求まります．

\begin{align} V_{out} = V_{ref} \times \left( \dfrac{R_5 + VR_3 + VR_1 + R_4}{R_5 + VR_3} \right) \end{align}

出力電流リミッタ

LT1172のVC端子の入力電圧を制御することで，出力電流を制限できます．VC端子は，LT1172内部で，誤差アンプの出力に接続されています．

VC端子の本来の役目は，位相補償ですが，この端子の電圧を変えれば，強制的にデューティを調節できます．

2次側のグラウンド・ラインに直列に挿入した電流検出抵抗$R_1$両端の電圧をOPアンプ LM358に入力し，基準電圧と比較します．差分を増幅して，VC端子の電圧を低下させることで，出力電流を一定値に制御します．

D$_3$は，定電圧動作時に，VC端子にOPアンプの出力が干渉しないようにするダイオードです．

LT1172の場合，デューティが0のとき制御電圧（Control Pin Threshold）の最低保証は0.6Vです．OPアンプで，0.6V以下まで確実に駆動するために，ダイオードに$V_F$の低いショットキー・バリアを使います．

出力電流制限値（$I_{OC}$）は，検出抵抗を$R_{SC}$，電流設定基準電圧を$V_{refC}$とすると次式で求まります．

\begin{align} I_{OC} = \dfrac{V_{refC}}{R_{SC}} \end{align}

電流設定基準電圧

出力電流リミッタの電流設定値を決める基準電圧源は，シャント・レギュレータIC LM431AのカソードとREF端子を接続して作ります．$R_{14}$と$VR_2$で分圧して，0～2.0Vの範囲で可変にします．

$R_{10}$と$R_8$で分圧して，電流検出OPアンプの基準電源とします．

$VR_2$を調節すると，出力電流を設定する基準電圧が変化して，出力電流を制限する定電流値を調整できます．

$R_{14}$と$VR_2$の分圧は，$VR_2$の設定位置によって，その出力インピーダンスが変化しますから，OPアンプを使ったバッファを挿入して，インピーダンスを下げます．こうすることで，$VR_2$が変化しても，電流制限基準電圧が影響を受けなくなります．

OPアンプLM358は2回路入りなので，1回路を誤差増幅にもう1回路を基準電圧のバッファ・アンプに使用します．

OPアンプの入力オフセット電圧が，出力電流が最大の0.3Aのとき，$R_{SC}$の両端に生じる電圧（$V_{SC}$）に対して十分小さい必要があります．さらに，$R_{SC}$の損失ができるだけ小さくなるようにします．今回は$V_{SC}$を0.25Vにしました．

基準電源は，$VR_2$を最大点に設定したとき2.0Vです．電流検出抵抗$R_{SC}$の値は次式から0.833$\Omega$です．

\begin{align} R_{SC} &= \dfrac{0.25 \mathrm{V}}{0.3 \mathrm{A}} = 0.833 \Omega \end{align}

この値に近いE12系列の標準抵抗値0.82$\Omega$を選びます．確認のため，$R_{SC}$=0.82$\Omega$のときの$R_{SC}$両端の電圧（$V_{SC}$）を求めると次式から0.246Vなので問題ありません．

\begin{align} V_{SC} = 0.3 \mathrm{A} \times 0.82 \Omega = 0.246 \mathrm{V} \end{align}

電流検出OPアンプの基準電圧が0.246Vになる$R_8$と$R_{10}$の分圧比を設定します．

$R_8$を1k$\Omega$と仮定すると，$R_{10}$は次のように求まります．

\begin{align} R_{10} = \dfrac{2 \mathrm{V}}{0.246 \mathrm{V}} \times 1 \rm{k} \Omega - 1 \rm{k} \Omega = 7.13 \rm{k} \Omega \end{align}

この抵抗値に近い標準抵抗値8.2k$\Omega$を採用します．8.2k$\Omega$と1k$\Omega$の分圧比で定電流値（$I_{SC}$）を求めると，次のようになります．

\begin{align} I_{SC} = \dfrac{\left(\dfrac{1 \rm{k} \Omega}{1 \rm{k} \Omega + 8.2 \rm{k} \Omega} \times 2 \mathrm{V}\right)}{0.82 \Omega} = 0.265 \mathrm{A} \end{align}

0.3Aより低めですが，試作確認では0.29A出力できました．理由はOPアンプのオフセットです．最適値は，24系列の抵抗$7.5k\Omega$です．

LT1172の入出力端子の逆バイアス防止

OPアンプ LM358の$V_{in+}$端子とグラウンド間のダイオード（D$_4$）は，出力端が短絡された場合に，$V_{in+}$端子がマイナスにバイアスされることを防ぐ働きがあります．

LM358は単電源でも動きます．$V_{CC}$端子は+5Vに，グラウンド端子は2次グラウンド・ラインに接続します．LM358の$V_{in}$端子に入力できる許容同相入力電圧範囲は，$-0.3$～$V_{CC}-2$Vです．

DC-DCコンバータの出力が短絡されると，電流検出抵抗に流れる電流が急増しますが，電源の制御系が電流を制限し始めるまでにタイムラグがあります．制限が効き始めるまでの期間，LM358の$V_{in}$端子には$-0.3$V以下の電圧が加わります．すると，OPアンプ内部の半導体チップのサブストレートとの間に逆バイアスが加わって寄生ダイオードや寄生トランジスタがONし，回路が動かなくなります．この現象を「ラッチアップ」と言います．

$V_{in-}$端子とグラウンドの間に，順方向電圧（$V_F$）の低いショットキー・バリア・ダイオードを追加してクランプすれば回避できます．

位相補償回路

OPアンプやLT1172の内蔵アンプの出力と，反転入力の間にあるキャパシタと抵抗は，動作を安定させるための位相補償回路です．

負帰還アンプは，入力に戻す信号の位相が，ある周波数で出力信号に対して180°遅れ，かつ，その周波数でのゲインが1以上あると発振します．

これを回避するためのテクニックが位相補償です．

ある周波数以上の増幅率を$R$と$C$を組み合わせた回路で調整します．

出力電圧検出回路と並列に接続された$R_3$と$C_{14}$の直列回路も一種の位相補償です．高い周波数帯域のゲインが低下すると，電源の過渡応答が悪くなります．そのため，比較的高い周波数で応答する進み補償を追加して，過渡応答と位相遅れを改善しています．

計算が複雑なので，カット・アンド・トライで，出力リプル波形を確認しながら定数を決めました．出力負荷を急変させ，応答波形にリンギングがなく，スムースに復帰するように決めます．

プリント基板の設計と製作

RSコンポーネント社のCADソフトウェア DESGINSPARK PCBを使いました．ユーザ登録すれだけで，誰でも無料で使えます．

図25に示すのは，本器のプリント基板のレイアウトです．プリント基板の寸法は87$\times$57mmです．

第6回　性能と考察

出力電圧-出力電流特性

5V出力時

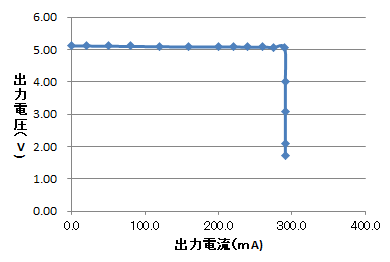
図26に示します．

完全な定電圧，定電流特性が得られています．定電流領域に入るまで＋5V一定で，291mAから垂下特性を示します．設計では，300mAで垂下特性を示すように狙いました．$R_{10}$の8.2k$\Omega$を6.8k$\Omega$にすれば0.31A前後になりますが，7.5k$\Omega$に変更するとちょうどよいです．

12V出力時

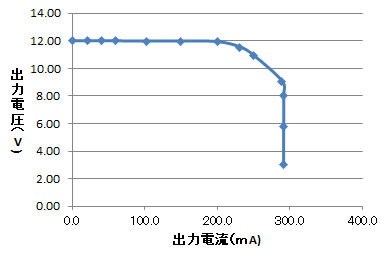
図27に示します．出力200mA以上で，出力電圧が徐々に低下します．LT1172内部の過電流検出回路でスイッチング電流のピークが約2.4Aで制限されるからです．完全ではありませんが定電力特性を示しています．出力291mAに達すると，5V出力時と同様に定電流特性になります．

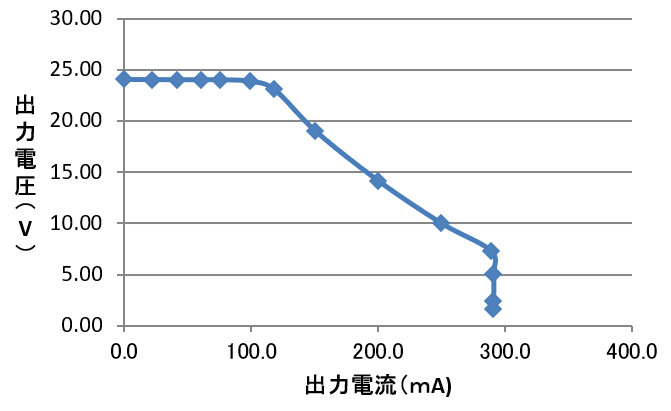
24V出力時

図28に示します．100mA付近から定電力特性に入ります．開始点の出力電力は2.4W（=24V$\times$100mA），12Vのときも2.4W（=12V$\times$200mA）です．つまり，本電源は，2.4W出力以下で使わないと定電圧特性が得られません．出力24Vで使うなら，定電流設定値は100mA以下です．

最大出力

本電源の入力電流仕様は，USB2.0の規定（500mA，2.5W）を超えています．USBバス・パワーの能力が500mAで制限されていると，2.4Wの電力を取り出すことはできません．USB2.0の規定に従うなら，最大出力は1.75Wです．

組み合わせるパソコンのUSBの出力によって，本電源の最大出力が決まります．

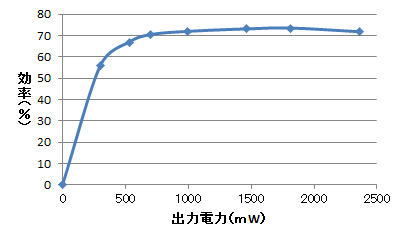
効率-出力電力特性

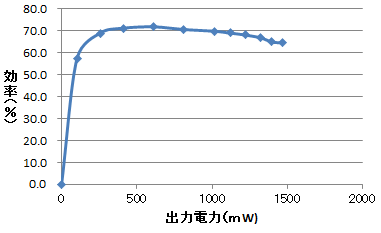
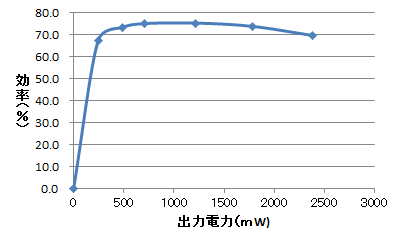
効率はおおむね70$\%$です．2.4W程度の小容量で，5Vと低い電圧で動くDC-DCコンバータとしては悪くありません．

図29に，5V出力時の効率-出力電力特性を示します．

図30に，12V出力時の効率-出力電力特性を示します．

図31に，24V出力時の効率-出力電力特性を示します．

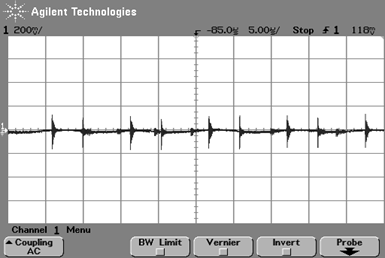
入力と出力のリプル・ノイズ

図32に，入力のライン間のリプル・ノイズを示します．

230mV$_{\rm{P-P}}$のノイズが観測されました．ノイズの多くは，コモン・モード・ノイズです．この程度ならパソコンへの影響はありません．

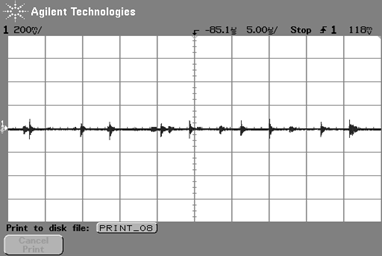
図33に，出力ライン間のリプル・ノイズを示します．

電圧は120mV$_{\rm{P-P}}$です．リプル・ノイズの一般的な大きさは，出力電圧の1$\%_{\rm{P-P}}$ですから標準的です．f

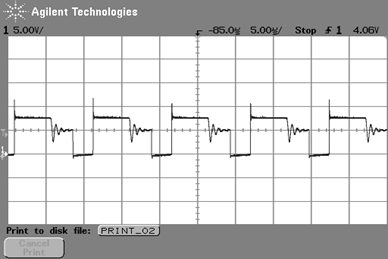
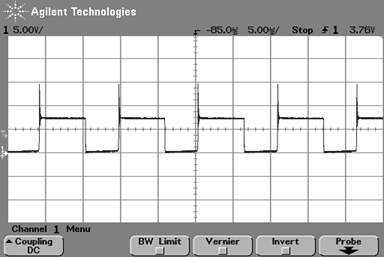
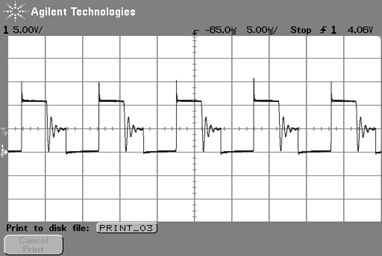
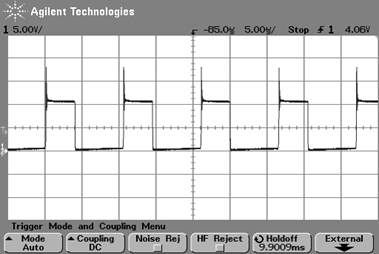
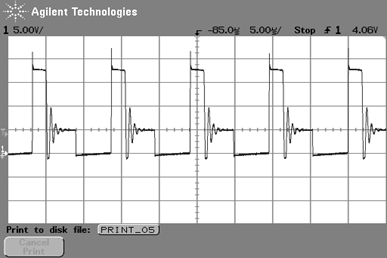
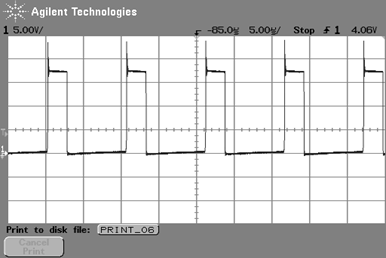
スイッチング波形$V_{DS}$

図34～図35は，制御IC LT1172のVSW端子のスイッチング波形です．負荷が重いときに観測されるのは，CCMモードで動作するフライバック方式でよくある典型的なスイッチング波形です．